【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
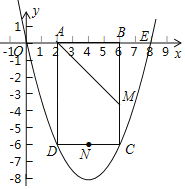
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
参考答案:
【答案】(1)y=![]() x2﹣4x;(2)四边形MNGF周长最小值为12
x2﹣4x;(2)四边形MNGF周长最小值为12![]() ;(3)存在点P,P坐标为(6,﹣6);(4)抛物线平移的距离为3个单位长度.
;(3)存在点P,P坐标为(6,﹣6);(4)抛物线平移的距离为3个单位长度.
【解析】
(1)由点E在x轴正半轴且点A在线段OE上得到点A在x轴正半轴上,所以A(2,0);由OA=2,且OA:AD=1:3得AD=6.由于四边形ABCD为矩形,故有AD⊥AB,所以点D在第四象限,横坐标与A的横坐标相同,进而得到点D坐标.由抛物线经过点D、E,用待定系数法即求出其解析式;(2)画出四边形MNGF,由于点F、G分别在x轴、y轴上运动,故可作点M关于x轴的对称点点M',作点N关于y轴的对称点点N',得FM=FM'、GN=GN'.易得当M'、F、G、N'在同一直线上时N'G+GF+FM'=M'N'最小,故四边形MNGF周长最小值等于MN+M'N'.根据矩形性质、抛物线线性质等条件求出点M、M'、N、N'坐标,即求得答案;(3)因为OD可求,且已知△ODP中OD边上的高,故可求△ODP的面积.又因为△ODP的面积常规求法是过点P作PQ平行y轴交直线OD于点Q,把△ODP拆分为△OPQ与△DPQ的和或差来计算,故存在等量关系.设点P坐标为t,用t表示PQ的长即可列方程.求得t的值要讨论是否满足点P在x轴下方的条件;(4)由KL平分矩形ABCD的面积可得K在线段AB上、L在线段CD上,画出平移后的抛物线可知,点K由点O平移得到,点L由点D平移得到,故有K(m,0),L(2+m,-6).易证KL平分矩形面积时,KL一定经过矩形的中心H且被H平分,求出H坐标为(4,﹣3),由中点坐标公式即求得m的值.
(1)∵点A在线段OE上,E(8,0),OA=2
∴A(2,0)
∵OA:AD=1:3
∴AD=3OA=6
∵四边形ABCD是矩形
∴AD⊥AB
∴D(2,﹣6)
∵抛物线y=ax2+bx经过点D、E
∴![]()
解得: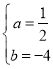
∴抛物线的解析式为y=![]() x2﹣4x
x2﹣4x
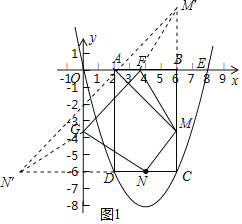
(2)如图1,作点M关于x轴的对称点M',作点N关于y轴的对称点N',连接FM'、GN'、M'N'
∵y=![]() x2﹣4x=
x2﹣4x=![]() (x﹣4)2﹣8
(x﹣4)2﹣8
∴抛物线对称轴为直线x=4
∵点C、D在抛物线上,且CD∥x轴,D(2,﹣6)
∴yC=yD=﹣6,即点C、D关于直线x=4对称
∴xC=4+(4﹣xD)=4+4﹣2=6,即C(6,﹣6)
∴AB=CD=4,B(6,0)
∵AM平分∠BAD,∠BAD=∠ABM=90°
∴∠BAM=45°
∴BM=AB=4
∴M(6,﹣4)
∵点M、M'关于x轴对称,点F在x轴上
∴M'(6,4),FM=FM'
∵N为CD中点
∴N(4,﹣6)
∵点N、N'关于y轴对称,点G在y轴上
∴N'(﹣4,﹣6),GN=GN'
∴C四边形MNGF=MN+NG+GF+FM=MN+N'G+GF+FM'
∵当M'、F、G、N'在同一直线上时,N'G+GF+FM'=M'N'最小
∴C四边形MNGF=MN+M'N'=![]()
∴四边形MNGF周长最小值为12![]() .
.
(3)存在点P,使△ODP中OD边上的高为![]() .
.
过点P作PQ∥y轴交直线OD于点Q
∵D(2,﹣6)
∴OD=![]() ,直线OD解析式为y=﹣3x
,直线OD解析式为y=﹣3x
设点P坐标为(t,![]() t2﹣4t)(0<t<8),则点Q(t,﹣3t)
t2﹣4t)(0<t<8),则点Q(t,﹣3t)
①如图2,当0<t<2时,点P在点D左侧

∴PQ=yQ﹣yP=﹣3t﹣(![]() t2﹣4t)=﹣
t2﹣4t)=﹣![]() t2+t
t2+t
∴S△ODP=S△OPQ+S△DPQ=![]() PQxP+
PQxP+![]() PQ(xD﹣xP)=
PQ(xD﹣xP)=![]() PQ(xP+xD﹣xP)=
PQ(xP+xD﹣xP)=![]() PQxD=PQ=﹣
PQxD=PQ=﹣![]() t2+t
t2+t
∵△ODP中OD边上的高h=![]() ,
,
∴S△ODP=![]() ODh
ODh
∴﹣![]() t2+t=
t2+t=![]() ×2
×2![]() ×
×![]()
方程无解
②如图3,当2<t<8时,点P在点D右侧
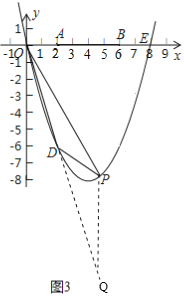
∴PQ=yP﹣yQ=![]() t2﹣4t﹣(﹣3t)=
t2﹣4t﹣(﹣3t)=![]() t2﹣t
t2﹣t
∴S△ODP=S△OPQ﹣S△DPQ=![]() PQxP﹣
PQxP﹣![]() PQ(xP﹣xD)=
PQ(xP﹣xD)=![]() PQ(xP﹣xP+xD)=
PQ(xP﹣xP+xD)=![]() PQxD=PQ=
PQxD=PQ=![]() t2﹣t
t2﹣t
∴![]() t2﹣t=
t2﹣t=![]() ×2
×2![]() ×
×![]()
解得:t1=﹣4(舍去),t2=6
∴P(6,﹣6)
综上所述,点P坐标为(6,﹣6)满足使△ODP中OD边上的高为![]() .
.
(4)设抛物线向右平移m个单位长度后与矩形ABCD有交点K、L
∵KL平分矩形ABCD的面积
∴K在线段AB上,L在线段CD上,如图4
∴K(m,0),L(2+m,-6)
连接AC,交KL于点H ∵S△ACD=S四边形ADLK= ∴S△AHK=S△CHL ∵AK∥LC ∴△AHK∽△CHL ∴ ∴AH=CH,KH=HL,即点H为AC中点,也是KL中点 ∴H(4,﹣3) ∴ ∴m=3 ∴抛物线平移的距离为3个单位长度.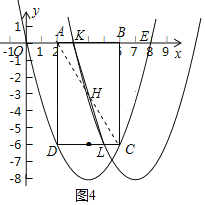
![]() S矩形ABCD
S矩形ABCD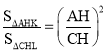 =
=![]() =1,
=1,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲
乙
进价(元/袋)
m
m﹣2
售价(元/袋)
20
13
(1)求m的值;
(2)假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)
-
科目: 来源: 题型:
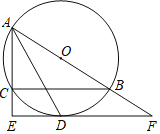
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=8,CE=4,求弧BD的长.(结果保留π)
-
科目: 来源: 题型:
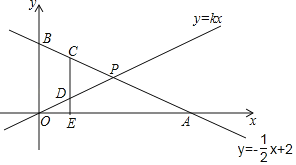
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=﹣
 x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
-
科目: 来源: 题型:
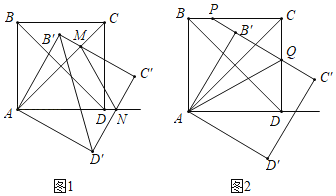
查看答案和解析>>【题目】如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.
(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;
(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.
①求∠DAQ的度数;
②若AB=6,求PQ的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】面对新冠肺炎疫情对经济运行的冲击,中国人民银行营业管理部(中国人民银行总行在京派驻机构)与相关部门多方动员,合力推动辖内9家全国性银行北京分行和3家地方法人银行为疫情防控重点企业提供优惠利率贷款,有力有序推动企业复工复产.截至2020年4月2日,已发放优惠利率贷款573笔,金额280 亿元.将280 亿元用科学记数法表示应为( )
A.28×
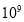 元B.2.8×
元B.2.8×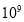 元C.2.8×
元C.2.8×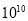 元D.2.8×
元D.2.8×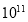 元
元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于
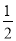 AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )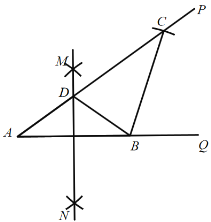
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
相关试题

