【题目】填空:如图,己知![]()
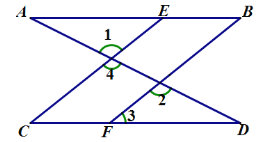
可推得![]() .理由如下:
.理由如下:
![]() (已知),
(已知),
又![]() ( )
( )
![]() ( )
( )
![]() ( )
( )
![]()
![]() ( )
( )
又![]() ( )
( )
![]() ( )
( )
![]() ( )
( )
参考答案:
【答案】对顶角线相等;等量代换;同位角相等,两直线平行;![]() ;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
【解析】
根据平行线的性质与判定即可求解.
∵∠1=∠2(已知),
又∵∠1=∠4(对顶角相等),
∴∠2=∠4 (等量代换),
∴CE∥BF (同位角相等,两直线平行),
∴∠C=∠3(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换),
∴AB∥CD (内错角相等,两直线平行).
故答案为:对顶角线相等;等量代换;同位角相等,两直线平行;![]() ;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
-
科目: 来源: 题型:
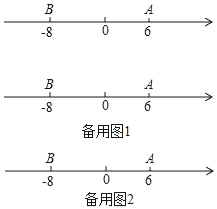
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别是6,﹣8,M、N、P为数轴上三个动点,点M从A点出发速度为每秒2个单位长度,点N从点B出发速度为点M的3倍,点P从原点出发速度为每秒1个单位长度.
(1)求A、B两点的距离为 个单位长度.
(2)若点M向右运动,同时点N向左运动,求经过多长时间点M与点N相距54个单位长度?
(3)若点M、N、P同时都向右运动,当点M与点N相遇后,点M、P继续以原来的速度向右运动,点N改变运动方向,以原来的速度向左运动,求从开始运动后,经过多长时间点P到点M、N的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、点D、线段BC,请用无刻度的直尺和圆规按下列要求与步骤画图:
(1)画直线AB;
(2)画射线DA;
(3)连接CD;
(4)延长线段BC至点E,使得CE=BC(请保留作图痕迹);
(5)在四边形ABCD内找一点O,使得OA+OB+OC+OD的值最小.
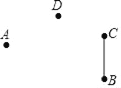
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
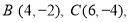
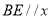 轴,点
轴,点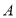 从原点
从原点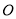 出发在
出发在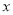 轴上以
轴上以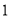 单位/秒的速度向
单位/秒的速度向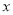 轴的正方向运动,运动的时间为
轴的正方向运动,运动的时间为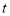 秒.
秒.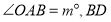 平分
平分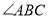 . (提示:
. (提示: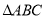 中,
中,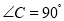 ,若
,若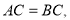 则
则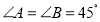 ,反之亦然)
,反之亦然)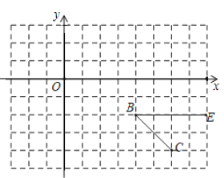
(1)当
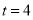 时,
时,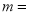 ;
;(2)当
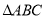 的面积为
的面积为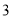 时,求
时,求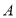 点运动的时间
点运动的时间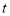 ;
;(3)当
 时,求
时,求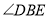 的度数(用含
的度数(用含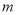 的式子表示,且不含绝对值).
的式子表示,且不含绝对值). -
科目: 来源: 题型:
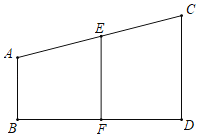
查看答案和解析>>【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB= ( )
∴∠ABD+∠CDB=180°
∴AB∥ ( )
又∠A与∠AEF互补 ( )
∠A+∠AEF=
∴AB∥ ( )
∴CD∥EF ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前全国提倡环保,节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1000只,这两种节能灯的进价,售价如下表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)如何进货,进货款恰好为37000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
相关试题

