【题目】背景阅读:
意大利著名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为裴波那契数列.
实践操作:
(1)写出裴波那契数列的前10个数;
(2)裴波那契数列的前2017个数中,有多少个奇数?
(3)现以这组数的各个数作为正方形的边长构造如图1的正方形系列:再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④、⑤……


(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号 | ① | ② | ③ | ④ | ⑤ | …… |
周长 | 6 | 10 | …… |
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形的面积和周长.
参考答案:
【答案】(1)1,1,2,3,5,8,13,21,34,55;(2)1345个;(3)i)16,26,42;i)面积:12816;周长:466
【解析】
(1)斐波那契数列的定义即可求解;
(2)分析婓波那契数列,可以发现每三项都是前两个为奇第三个为偶,结合2017是3的多少倍余几,即可得出结论;
(3)①根据图形特性,可以找出周长为最大的正方形的周长+小一号的正方形的两条边,代入数据即可得出结论;
②先得到序号为⑩的长方形长为144,宽为89,再根据长方形的面积和周长公式即可求解.
(1)写出斐波那契数列的前10个数是:1,1,2,3,5,8,13,21,34,55
(2)奇偶特点:奇,奇,偶,奇,奇,偶,奇,奇,偶……,3个一周期.
![]()
奇数:![]() (个)
(个)
(3)(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号 | ① | ② | ③ | ④ | ⑤ | …… |
周长 | 6 | 10 | 16 | 26 | 42 | …… |
(ii)宽:89,长:144;
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
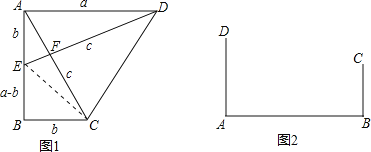
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式
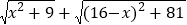 最小值(0<x<16)
最小值(0<x<16) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=
 计算.解答下列问题:
计算.解答下列问题:(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
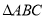 是等腰直角三角形,其中
是等腰直角三角形,其中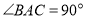 ,
,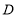 是
是 边上的一点,连接
边上的一点,连接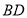 ,过
,过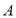 作
作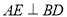 交
交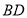 于
于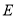 ,
,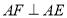 ,且
,且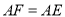 ,连接
,连接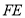 并延长,交
并延长,交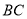 于
于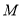 点.若四边形
点.若四边形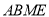 的面积为
的面积为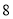 ,则
,则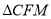 的面积为__________.
的面积为__________.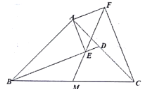
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3,第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=_____个单位长度.

相关试题

