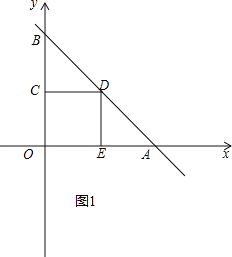
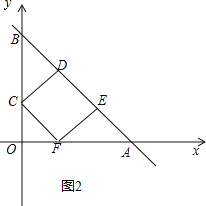
【题目】在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,则此正方形落在x轴正半轴的顶点坐标为 .
参考答案:
【答案】(1.5,0)或(1,0).
【解析】
试题分析:分两种情况:①如图1,令x=0,则y=3,令y=0,则x=3,得到OA=OB=3,∠BAO=45°,根据DE⊥OA,推出DE=AE,由于四边形COED是正方形,得到OE=DE,等量代换得到OE=AE,即可得到结论;②如图2,由(1)知△OFC,△EFA是等腰直角三角形,由四边形CDEF是正方形,得到EF=CF,于是得到AF=![]() ×
×![]() OF=2OF,求出OA=OF+2OF=3,即可得到结论.
OF=2OF,求出OA=OF+2OF=3,即可得到结论.
解:分两种情况;
①如图1,令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=![]() OA=1.5,
OA=1.5,
∴E(1.5,0);
②如图2,由①知△OFC,△EFA是等腰直角三角形,
∴CF=![]() OF,AF=
OF,AF=![]() EF,
EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=![]() ×
×![]() OF=2OF,
OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
故答案为(1.5,0)或(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+y=4的解是( )
A.
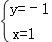 B.
B.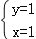 C.
C.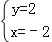 D.
D.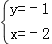
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,则DE的长是( )
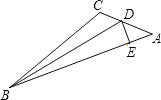
A.4.8cm B.4.5cm C.4cm D.2.4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别
捐款额(x)元
户数
A
1≤x<50
a
B
50≤x<100
10
C
100≤x<150
D
150≤x<200
E
x≥200
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】江苏省占地面积约为107200平方公里.将107200用科学记数法表示应为( )
A.0.1072×106 B.1.072×105 C.1.072×106 D.10.72×104
-
科目: 来源: 题型:
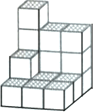
查看答案和解析>>【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.

(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
相关试题

