搜索
【题目】“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形．如果小正方形的面积为4，大正方形的面积为100，直角三角形中较小的锐角为α，则tanα的值等于____
参考答案：
【答案】
【解析】由题意知小正方形的边长为2，大正方形的边长为10．设直角三角形中较小边长为x，则有（x+2）2+x2=102，解方程求得x=6，从而求出较长边的长度．运用正切函数定义求解．
解：由题意知，小正方形的边长为2，大正方形的边长为10．
设直角三角形中较小边长为x，
则有（x+2）2+x2=102，
解得，x=6．
∴较长边的边长为x+2=8．
∴tanα=短边：长边=6：8=
．
此题首先要求学生正确理解题意，然后会利用勾股定理和锐角三角函数的概念解题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点P在AB边上，AE⊥DP于E点，CF⊥DP于F点，若AE＝5，CF＝9，则EF＝_______．
-
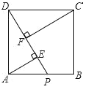
科目： 来源： 题型：
查看答案和解析>>【题目】【问题学习】小芸在小组学习时问小娟这样一个问题：已知α为锐角，且sin α＝
，求sin 2α的值．小娟是这样给小芸讲解的：
如图①，在⊙O中，AB是直径，点C在⊙O上，所以∠ACB＝90°. 设∠BAC＝α，则sin α＝
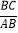＝.易得∠BOC＝2α.设BC＝x，则AB＝3x，AC＝2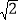
x.作CD⊥AB于D，求出CD＝________(用含x的式子表示)，可求得sin 2α＝
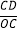＝________.【问题解决】已知，如图②，点M，N，P为⊙O上的三点，且∠P＝β，sin β＝
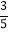，求sin 2β的值．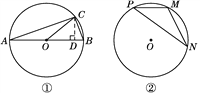
-
科目： 来源： 题型：
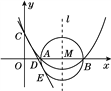
查看答案和解析>>【题目】如图，已知抛物线
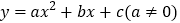的顶点坐标为
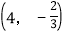，且与y轴交于点C(0，2)，与x轴交于A，B两点(点A在点B的左边)．(1)求抛物线的表达式及A，B两点的坐标．
(2)在(1)中抛物线的对称轴l上是否存在一点P，使AP＋CP的值最小？若存在，求AP＋CP的最小值；若不存在，请说明理由；
(3)在以AB为直径的⊙M中，CE与⊙M相切于点E，CE交x轴于点D，求直线CE的表达式．
-
科目： 来源： 题型：
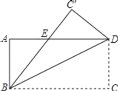
查看答案和解析>>【题目】如图，矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于点E，AD=4，AB=3，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．
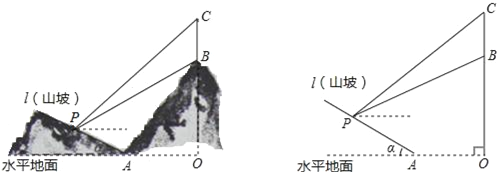
求：
（1）P到OC的距离．
（2）山坡的坡度tanα．
（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin31°≈0.52，tan31°≈0.60）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
（1）如图（1），若∠AOC=
，求∠DOE的度数；（2）如图（2），将∠COD绕顶点O旋转，且保持射线OC在直线AB上方，在整个旋转过程中，当∠AOC的度数是多少时，∠COE=2∠DOB．
相关试题
