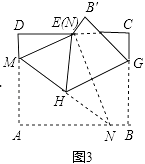
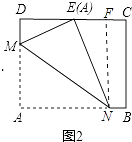
【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 
参考答案:
【答案】![]()
![]()
【解析】解:如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x,
∵DE=EC,AB=CD=8 ![]() ,
,
∴DE= ![]() CD=4
CD=4 ![]() ,
,
在RT△DEM中,∵DM2+DE2=EM2 ,
∴(4 ![]() )2+x2=(10﹣x)2 ,
)2+x2=(10﹣x)2 ,
解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEN+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EN= ![]()
![]() ,
,
∴AN=EN= ![]()
![]() ,
,
∴tan∠AMN= ![]() =
= ![]()
![]() ,
,
如图3中,∵ME⊥EN,HG⊥EN,
∴EM∥GH,
∴∠NME=∠NHK,
∵∠NME=∠AMN,∠EHG=∠NHK,
∴∠AMN=∠EHG,
∴tan∠EHG=tan∠AMN= ![]()
![]() .
.
所以答案是 ![]()
![]() .
.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )

A.
B.4
C.2
D.
-
科目: 来源: 题型:
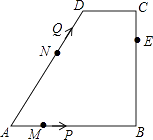
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.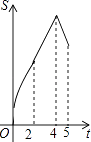
B.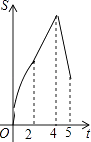
C.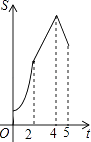
D.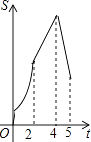
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt
 中,
中, ,分别以点A、C为圆心,大于
,分别以点A、C为圆心,大于 长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.(1)求
 ;(直接写出结果)
;(直接写出结果)(2)当AB=3,AC=5时,求
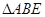 的周长.
的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)先化简再求值:a(1﹣4a)+(2a+1)(2a﹣1),其中a=4.
(2)解不等式组: .
. -
科目: 来源: 题型:
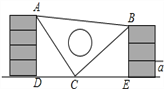
查看答案和解析>>【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
相关试题

