【题目】有一块直角三角形的绿地,量得两直角边长分别为5m,12m.现在要将绿地扩充成等腰三角形绿地,且扩允部分是以12m为直角边的直角三角形,求扩充部分三角形绿地的面积.(如图备用)

参考答案:
【答案】扩充后等腰三角形绿地的面积是30m2或48m2或71.4m2.
【解析】
根据勾股定理求出斜边AB, (1) 当AB=AD时或AB=BD,求出CD即可; (2) 当AB=BD时,求出CD、AD,即可求出△ABD的面积; (3) 当DA=DB时,设AD=x,则CD=x-5,根据勾股定理,列出方程,求出x,即可求出△ABD的面积;
解:
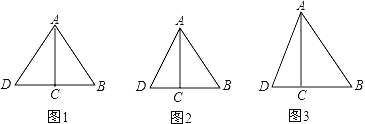
在Rt△ABC中,∵∠ACB=90°,AC=5m,BC=12m,
∴AB=13m,
(1)如图1,当AB=AD时,CD=5m,
则△ABD的面积为: ![]()
若延长AC到D,使CD=AC=12m,则△ABD的面积为![]()
60﹣30=30 (m2);
(2)图2,当AB=BD时,CD=8m,则△ABD的面积为:![]()
78﹣30=48(m2);
(3)如图3,当DA=DB时,设AD=x,则CD=x﹣5,
则![]() ,
,
∴x=16.9,
则△ABD的面积为: ![]()
101.4﹣30=71.4(m2);
答:扩充后等腰三角形绿地的面积是30m2或60m2或71.4m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
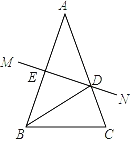
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
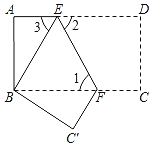
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=55°,求∠2、∠3的度数;
(3)若AB=6,AD=12,求△BC′F的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC

 ,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.(1)求证:
 ;
;(2)若GE=2,BF=3,求线段EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD为AB边上的高,AD=8,CD=4,BD=3.动点P从点A出发,沿射线AB运动,速度为1个单位/秒,运动时间为t秒.
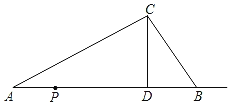
(1)当t为何值时,△PDC≌△BDC;
(2)当t为何值时,△PBC是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
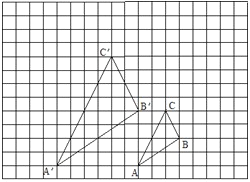
(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
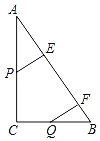
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
相关试题

