【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:

①b2﹣4ac>0;
②2a+b<0;
③4a﹣2b+c=0;
④a:b:c=﹣1:2:3.
其中正确的个数是( )
A.1 B.2 C.3 D.4
参考答案:
【答案】B.
【解析】
试题分析:∵二次函数y=ax2+bx+c(a≠0)的图象和x轴有两个交点,
∴b2-4ac>0,∴①正确;
∵二次函数的对称轴是直线x=1,
即二次函数的顶点的横坐标为x=-![]() =1,
=1,
∴2a+b=0,∴②错误;
把x=-2代入二次函数的解析式得:y=4a-2b+c,
从图象可知,当x=-2时,y<0,
即4a-2b+c<0,∴③错误;
∵二次函数的图象和x轴的一个交点时(-1,0),对称轴是直线x=1,
∴另一个交点的坐标是(3,0),
∴设y=ax2+bx+c=a(x-3)(x+1)=ax2-2ax-3a,
即a=a,b=-2a,c=-3a,
∴a:b:c=a:(-2a):(-3a)=-1:2:3,
∴④正确;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
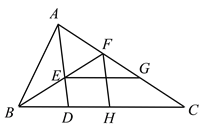
查看答案和解析>>【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
⑴求证:AE=FH;
⑵作EG//BC交AC于点G若AG=5,AC=8,求FG的长.
-
科目: 来源: 题型:
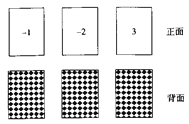
查看答案和解析>>【题目】如图所示,有3张不透明的卡片,除正面写有不同的数字外,其他均相同。将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b。
(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图像经过二、三、四象限的概率(用树状图或列表法求解)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:m2﹣9=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地一天早晨的气温是﹣5℃,中午上升了10℃,午夜又下降了8℃,则午夜的气温是( )
A.﹣3℃
B.﹣5℃
C.5℃
D.﹣9℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段的长为边,能组成三角形的是( )
A.2cm,3cm,4cm
B.2cm,3cm,5cm
C.2cm,5cm,10cm
D.8cm,4cm,4cm
相关试题

