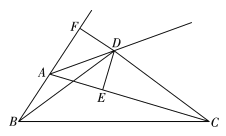
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据角平分线上的点到角的两边距离相等可得DE=DF,再利用“HL”证明Rt△CDE和Rt△BDF全等;根据全等三角形对应边相等可得CE=AF,利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,然后求出CE=AB+AE;根据全等三角形对应角相等可得∠DBF=∠DCE,然后求出A、B、C、D四点共圆,根据同弧所对的圆周角相等可得∠BDC=∠BAC;∠DAE=∠CBD,再根据全等三角形对应角相等可得∠DAE=∠DAF,然后求出∠DAF=∠CBD,进而得出∠ADF=∠CDB,不能得出∠ADF=∠CDE.
解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,
![]()
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF,
在Rt△ADE和Rt△ADF中,
![]()
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE,
∴A、B、C、D四点共圆,
∴∠BDC=∠BAC,故④正确;
∠DAE=∠CBD,
∵Rt△ADE≌Rt△ADF,
∴∠DAE=∠DAF,
∴∠DAF=∠CBD,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠ADF=∠CAD,
∴∠ADF≠∠CDE,故③错误;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1)解不等式
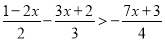 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.(2)解方程组:
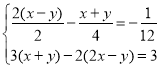 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是中心对称,又是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次列车平均提速
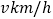 ,用相同的时间,列车提速前行驶
,用相同的时间,列车提速前行驶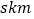 ,提速后比提速前多行驶
,提速后比提速前多行驶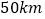 ,提速前列车的平均速度为多少?若设提速前这次列车的平均速度为
,提速前列车的平均速度为多少?若设提速前这次列车的平均速度为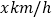 ,则根据行驶时间的等量关系可以列出的方程为( )
,则根据行驶时间的等量关系可以列出的方程为( )A.
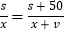 B.
B. 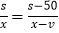 C.
C. 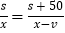 D.
D. 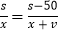
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元?
(2)为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
相关试题

