【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
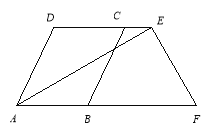
(1)、求证:DC//AB. (2)、求∠AFE的大小.
参考答案:
【答案】(1)、证明过程见解析;(2)、60°
【解析】
试题分析:(1)、根据AD∥BC得出∠ABC+∠DAB=180°,根据∠DCB=∠DAB得出∠ABC+∠DCB=180°,从而得出直线平行;(2)、根据AE⊥EF得出∠AEF=90°,从而说明∠DEF=120°,根据平行线的性质得出∠AFE的度数.
试题解析:(1)∵AD//BC ∴∠ABC+∠DAB=180°° ∵∠DCB=∠DAB ∴∠ABC+∠DCB=180° ∴DC//AB;
(2)、∵AE⊥EF, ∴∠AEF=90° ∵∠DEA=30° ∴∠DEF=30°+ 90° =120° ∵DC//AB
∴∠DEF+∠F=180° ∴∠AFE=60°
-
科目: 来源: 题型:
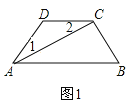
查看答案和解析>>【题目】 (1)、如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
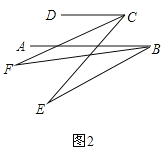
(2)如图,在(1)的条件下,AB的下方两点E,F满足:BF平分∠ABE,CF 平分∠DCE,若∠CFB=20°,∠DCE=70°,求∠ABE的度数
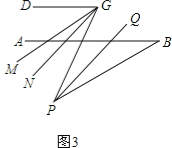
(3)在前面的条件下,若P是BE上一点;G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP﹣∠MGN的值不变;②∠MGN 的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
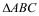 与
与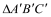 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.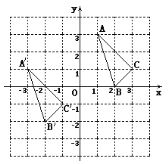
⑴、分别写出下列各点的坐标:
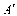 ;
; 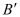 ;
; ;
;⑵、说明
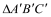 由
由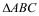 经过怎样的平移得到? .
经过怎样的平移得到? .⑶、若点
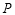 (
( ,
,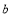 )是
)是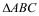 内部一点,则平移后
内部一点,则平移后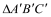 内的对应点
内的对应点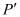 的坐标为 ;
的坐标为 ;⑷、求
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据威海市旅游局统计,今年“五·一”小长假期间,我市各旅游景点门票收入约2300万元,数据“2300万”用科学记数法表示为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2016°,则n等于( )
A. 11 B. 12 C. 13 D. 14
相关试题

