搜索
【题目】已知：如图所示，△AMN的周长为18，∠B，∠C的平分线相交于点O，过O点的直线MN∥BC交AB、AC于点M、N．则AB+AC= ．
参考答案：
【答案】18
【解析】试题分析：由∠B，∠C的平分线相交于点O，过O点的直线MN∥BC交AB、AC于点M、N，易证得△BOM与△CON是等腰三角形，继而可得AB+AC=△AMN的周长．
试题解析：∵MN∥BC， ∴∠BOM=∠OBC，∠CON=∠OCB， ∵∠B，∠C的平分线相交于点O，
∴∠MBO=∠OBC，∠NCO=∠OCB， ∴∠MBO=∠BOM，∠NCO=∠CON， ∴BM=OM，CN=ON，
∵△AMN的周长为18， ∴AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=18．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果|a+1|+（b﹣2）2=0，求（a+b）2009+a2008的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：规定“”是一种运算符号，且ab=ab﹣ba，如：23=23﹣32=8﹣9=﹣1，试计算：
（1）42
（2）4（32）的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列命题：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②三角形的三边a、b、c满足a2+c2=b2，则∠C=90°；
③△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
④△ABC中，若 a：b：c=1：2：
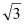，则这个三角形是直角三角形．其中，假命题的个数为（ ）
A．1个 B．2个 C．3个 D．4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：抛物线y=x2+bx+c经过点（2，-3）和（4，5）.
（1）求抛物线的表达式及顶点坐标；
（2）将抛物线沿x轴翻折，得到图象G，求图象G的表达式；
（3）在（2）的条件下，当-2<x<2时，直线y=m与该图象有一个公共点，求m的值或取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】正六边形的每个外角是度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个多边形的内角和是外角和的4倍还多180°，求这个多边形的边数．
相关试题
