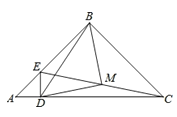
【题目】已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)当点E运动多少秒时,△BMD的面积为12.5cm2?
参考答案:
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BM=![]() CE,DM=
CE,DM=![]()
CE,得出BM=DM,再由等腰三角形的性质和三角形的外角性质证出∠BMD=90°即可;
(2)由等腰直角三角形的面积求出BM,得出CE,由勾股定理求出BE,得出AE,即可得出结果.
试题解析:(1)∵∠ABC=90°,DE⊥AC,点M为EC的中点,AB=BC,
∴BM=![]() CE=CM,DM=
CE=CM,DM=![]() CE=CM,∠BAC=∠ACB=45°,
CE=CM,∠BAC=∠ACB=45°,
∴BM=DM,∠MBC=∠MCB,∠MDC=∠MCD,
∵∠BME=∠MBC+∠MCB,∠DME=∠MDC+∠MCD,∠MCB+∠MCD=∠ACB=45°,
∴∠BMD=∠BME+∠DME=45°+45°=90°,
∴△BMD为等腰直角三角形;
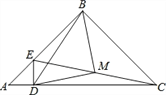
(2)由(1)得:△BMD为等腰直角三角形,
∴△BMD的面积=![]() BMDM=
BMDM= ![]() BM2=12.5,解得:BM=5,
BM2=12.5,解得:BM=5,
∴CE=2BM=10cm,由勾股定理得:BE= ![]() =6(cm),
=6(cm),
∴AE=AB﹣BE=2cm,∴2÷1=2(s),
即当点E运动2秒时,△BMD的面积为12.5cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角比它的余角的3倍多30°,这个角的度数是_______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.梯形的对角线相等
B.菱形的对角线不相等
C.矩形的对角线不能相互垂直
D.平行四边形的对角线可以互相垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知,3的正整数次幂:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,观察归纳,可得32007的个位数字是( )
A.1
B.3
C.7
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果(anbmb)3=a9b15,那么( )
A. m=4,n=3 B. m=4,n=4 C. m=3,n=4 D. m=3,n=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2的算术平方根为-a,则a的取值范围是( )
A. a>0B. a≥0C. a<0D. a≤0
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图.
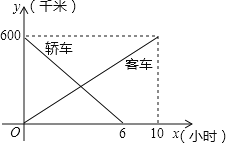
(1)根据图象,直接写出y1、y2关于x的函数关系式;
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间.
相关试题

