【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

参考答案:
【答案】(1)证明见解析;(2)4.9.
【解析】试题分析:(1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)∵∠B=90°,AB=12,BM=5,
∴AM=![]() =13,AD=12,
=13,AD=12,
∵F是AM的中点,
∴AF=![]() AM=6.5,
AM=6.5,
∵△ABM∽△EFA,
∴![]() ,
,
即![]() ,
,
∴AE=16.9,
∴DE=AE-AD=4.9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6 B.(a3)2=a5 C.(3ab2)3=9a3b6 D.a6÷a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
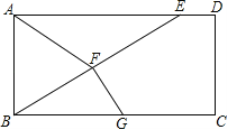
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长分别为3cm和6cm,则该等腰三角形的周长是( )
A.9cm
B.12cm
C.12cm或15cm
D.15cm -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3ma﹣6mb=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC三边之比为5:12:13,则△ABC是三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如果①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
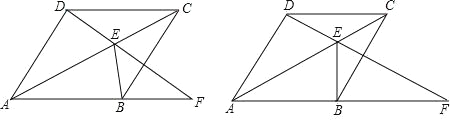
相关试题

