【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于点F,则下列说法正确的有( ) ①AE=CF;②EC+CF=4 ![]() ;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.
;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.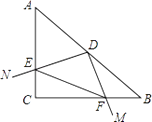
A.①②
B.①③
C.①②③
D.①②③④
参考答案:
【答案】D
【解析】解:①连接CD. 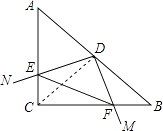
∵在Rt△ABC中,∠C=90°,AC=BC,点D为AB的中点,
∴CD⊥AB,CD=AD=DB,
在△ADE与△CDF中,∠A=DCF=45°,AD=CD,∠ADE=∠CDF,
∴△ADE≌△CDF,
∴AE=CF.说法正确;
②∵在Rt△ABC中,∠C=90°,AC=BC,AB=8,
∴AC=BC=4 ![]() .
.
由①知AE=CF,
∴EC+CF=EC+AE=AC=4 ![]() .说法正确;
.说法正确;
③由①知△ADE≌△CDF,
∴DE=DF.说法正确;
④∵△ECF的面积= ![]() ×CE×CF,如果这是一个定值,则CECF是一个定值,
×CE×CF,如果这是一个定值,则CECF是一个定值,
又∵EC+CF=4 ![]() ,
,
∴可唯一确定EC与EF的值,
再由勾股定理知EF的长也是一个定值,说法正确.
故选D.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以OA为斜边作等腰直角△OAB,再以OB为斜边在△OAB外侧作等腰直角△OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHI的面积比值是( )
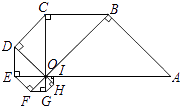
A.32
B.64
C.128
D.256 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
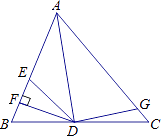
A.11
B.5.5
C.7
D.3.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+6x﹣7=0的解为( )
A. x1=1,x2=7B. x1=﹣1,x2=7
C. x1=﹣1,x2=﹣7D. x1=1,x2=﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数1,1,2,3,5,8,13是“斐波那契数列”的一部分,若去掉其中的两个数后这组数的中位数、众数保持不变,则去掉的两个数可能是( )
A. 2,5B. 1,5C. 2,3D. 5,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(5×103)×(20×10m)×(4×102)=4×109,则m的值为( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种运动鞋每双按成本价提高25%后标价,后因处理库存每双按标价的9折出售,若毎双鞋的出售价是90元,则每双鞋的成本价是元.
相关试题

