【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( ) 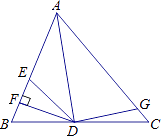
A.11
B.5.5
C.7
D.3.5
参考答案:
【答案】B
【解析】解:作DM=DE交AC于M,作DN⊥AC于点N, ∵DE=DG,
∴DM=DG,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DN,
在Rt△DEF和Rt△DMN中,![]() ,
,
∴Rt△DEF≌Rt△DMN(HL),
∵△ADG和△AED的面积分别为50和39,
∴S△MDG=S△ADG﹣S△ADM=50﹣39=11,
S△DNM=S△EDF= ![]() S△MDG=
S△MDG= ![]() ×11=5.5.
×11=5.5.
故选B.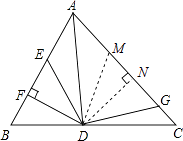
作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
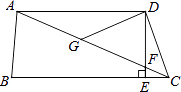
A.2
B.
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
-
科目: 来源: 题型:
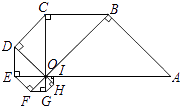
查看答案和解析>>【题目】以OA为斜边作等腰直角△OAB,再以OB为斜边在△OAB外侧作等腰直角△OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHI的面积比值是( )
A.32
B.64
C.128
D.256 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+6x﹣7=0的解为( )
A. x1=1,x2=7B. x1=﹣1,x2=7
C. x1=﹣1,x2=﹣7D. x1=1,x2=﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于点F,则下列说法正确的有( ) ①AE=CF;②EC+CF=4
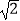 ;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.
;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.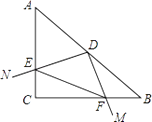
A.①②
B.①③
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数1,1,2,3,5,8,13是“斐波那契数列”的一部分,若去掉其中的两个数后这组数的中位数、众数保持不变,则去掉的两个数可能是( )
A. 2,5B. 1,5C. 2,3D. 5,8
相关试题

