Question

【题目】如图，已知抛物线经过A（3，0），B（0，3）两点．

（1）求此抛物线的解析式和直线AB的解析式；

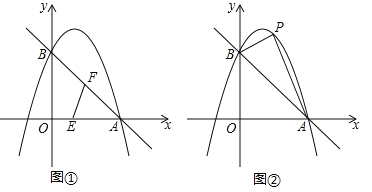
（2）如图①，动点E从O点出发，沿着OA方向以1个单位/秒的速度向终点A匀速运动，同时，动点F从A点出发，沿着AB方向以个单位/秒的速度向终点B匀速运动，当E，F中任意一点到达终点时另一点也随之停止运动，连接EF，设运动时间为t秒，当t为何值时，△AEF为直角三角形？

（3）如图②，取一根橡皮筋，两端点分别固定在A，B处，用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动，动点P与A，B两点构成无数个三角形，在这些三角形中是否存在一个面积最大的三角形？如果存在，求出最大面积，并指出此时点P的坐标；如果不存在，请简要说明理由．

Answer 1

【答案】（1），y=﹣x+3；（2）；（3）存在面积最大，最大是，此时点P（，）．

【解析】

试题分析：（1）用待定系数法求出抛物线，直线解析式；

（2）分两种情况进行计算即可；

（3）确定出面积达到最大时，直线PC和抛物线相交于唯一点，从而确定出直线PC解析式，根据锐角三角函数求出BD，计算即可．

试题解析：（1）∵抛物线经过A（3，0），B（0，3）两点，∴，∴，∴，设直线AB的解析式为y=kx+n，∴，∴，∴y=﹣x+3；

（2）由运动得，OE=t，AF=t，∴AE=OA﹣OE=3﹣t，∵△AEF为直角三角形，∴①△AOB∽△AEF，∴，∴，∴t=，②△AOB∽△AFE，∴，∴，∴t=；

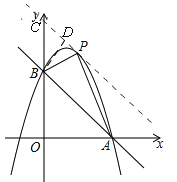
（3）如图，存在，过点P作PC∥AB交y轴于C，∵直线AB解析式为y=﹣x+3，∴设直线PC解析式为y=﹣x+b，联立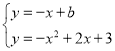，∴，∴，∴△=9﹣4（b﹣3）=0，∴b=，∴BC=﹣3=，x=，∴ P（，）．

过点B作BD⊥PC，∴直线BD解析式为y=x+3，∴BD=，∴BD=，∵AB=，S最大=AB×BD==．

即：存在面积最大，最大是，此时点P（，）．