【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

参考答案:
【答案】(1)12;(2)反比例函数的解析式为y=![]() ;一次函数的解析式为y=-
;一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得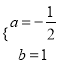 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD,AE分别是等边三角形ABC的高和中线,则AD 与AE 的大小关系为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则
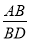 的值为( )
的值为( )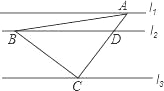
A.
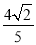 B.
B. 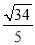 C.
C. 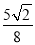 D.
D. 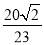
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O1的半径为3,⊙O2的半径为r,⊙O1与⊙O2只能画出两条不同的公共切线,且O1O2=5,则⊙O2的半径为r的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①点A、B关于x轴对称;②点A、B关于y轴对称;③A、B关于原点对称;④点A、B之间的距离为4,其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个三角形有两个角对应相等,正确的说法是( )
A. 两个三角形全等B. 如果一对等角的角平分线相等,两三角形就全等
C. 两个三角形一定不全等D. 如果还有一个角相等,两三角形就全等
相关试题

