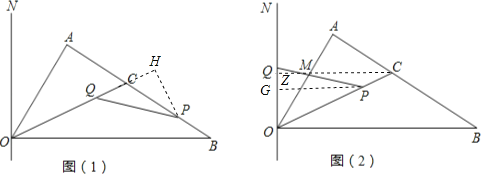
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

参考答案:
【答案】(1)OC=2,BC=2;(2)S与t的函数关系式是:S= ;(3)当t为
;(3)当t为![]() 或
或![]() 时,△OPM是等腰三角形.
时,△OPM是等腰三角形.
【解析】整体分析:
(1)先求出OA,判断OC=CB,再在Rt△AOC中用勾股定理列方程求解;(2)分点P在BC上,与点C重合,在CO上,与点O重合四种情况分类讨论,注意画出相应的图形,利用三角形的面积公式和三角形面积的和差关系求解;(3)因为等腰三角形的腰不确定,所以需要分三种情况讨论,利用等腰三角形的性质列方程求解.
(1)解:∵∠A=90°,∠AOB=60°,OB=2![]() ,
,
∴∠B=30°,∴OA=![]() OB=
OB=![]() ,
,
由勾股定理得:AB=3,
∵OC平分∠AOB,∴∠AOC=∠BOC=30°=∠B,∴OC=BC,
在△AOC中,AO2+AC2=CO2,∴(![]() )+(3﹣OC)2=OC2,∴OC=2=BC,
)+(3﹣OC)2=OC2,∴OC=2=BC,
答:OC=2,BC=2.
(2)解:①当P在BC上,Q在OC上时,0<t<2,则CP=2﹣t,CQ=t,
过P作PH⊥OC于H,∴∠HCP=60°,∠HPC=30°,
∴CH=![]() CP=
CP=![]() (2﹣t),HP=
(2﹣t),HP=![]() (2﹣t),
(2﹣t),
∴S△CPQ=![]() CQ×PH=
CQ×PH=![]() ×t×
×t×![]() (2﹣t),
(2﹣t),
即S=﹣![]() t2+
t2+![]() t;
t;
②当t=2时,P在C点,Q在O点,此时,△CPQ不存在,
∴S=0,
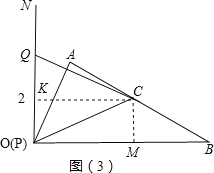
③当P在OC上,Q在ON上时2<t<4,
<>过P作PG⊥ON于G,过C作CZ⊥ON于Z,∵CO=2,∠NOC=60°,∴CZ=![]() ,CP=t﹣2,OQ=t﹣2,∠NOC=60°,
,CP=t﹣2,OQ=t﹣2,∠NOC=60°,
∴∠GPO=30°,∴OG=![]() OP=
OP=![]() (4﹣t),PG=
(4﹣t),PG=![]() (4﹣t),
(4﹣t),
∴S△CPQ=S△COQ﹣S△OPQ=![]() ×(t﹣2)×
×(t﹣2)×![]() ﹣
﹣![]() ×(t﹣2)×
×(t﹣2)×![]() (4﹣t),
(4﹣t),
即S=![]() t2﹣
t2﹣![]() t+
t+![]() .
.
④当t=4时,P在O点,Q在ON上,如图(3)
过C作CM⊥OB于M,CK⊥ON于K,
∵∠B=30°,由(1)知BC=2,∴CM=![]() BC=1,
BC=1,
有勾股定理得:BM=![]() ,
,
∵OB=2![]() ,∴OM=2
,∴OM=2![]() ﹣
﹣![]() =
=![]() =CK,∴S=
=CK,∴S=![]() PQ×CK=
PQ×CK=![]() ×2×
×2×![]() =
=![]() ;
;
综合上述:S与t的函数关系式是:S=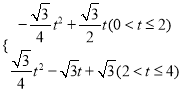 ;
;
(3)解:如图(2),∵ON⊥OB,∴∠NOB=90°,
∵∠B=30°,∠A=90°,∴∠AOB=60°,
∵OC平分∠AOB,∴∠AOC=∠BOC=30°,∴∠NOC=90°﹣30°=60°,
①OM=PM时,∠MOP=∠MPO=30°,
∴∠PQO=180°﹣∠QOP﹣∠MPO=90°,
∴OP=2OQ,∴2(t﹣2)=4﹣t,解得:t=![]() ,
,
②PM=OP时,∠PMO=∠MOP=30°,
∴∠MPO=120°,∵∠QOP=60°,∴此时不存在;
③OM=OP时,过P作PG⊥ON于G,OP=4﹣t,∠QOP=60°,
∴∠OPG=30°,∴GO=![]() (4﹣t),PG=
(4﹣t),PG=![]() (4﹣t),
(4﹣t),
∵∠AOC=30°,OM=OP,∴∠OPM=∠OMP=75°,
∴∠PQO=180°﹣∠QOP﹣∠QPO=45°,∴PG=QG=![]() (4﹣t),
(4﹣t),
∵OG+QG=OQ,∴ ![]() (4﹣t)+
(4﹣t)+![]() (4﹣t)=t﹣2,解得:t=
(4﹣t)=t﹣2,解得:t=![]()
综合上述:当t为![]() 或
或![]() 时,△OPM是等腰三角形.
时,△OPM是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;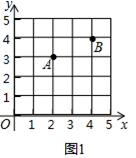
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.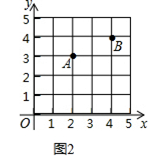
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D

(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③AD=4AG; ④FH=
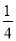 BD
BD其中正确的结论有( ).
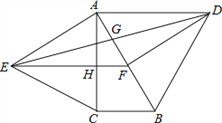
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过抛物线y=
 x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
相关试题

