【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③AD=4AG; ④FH=![]() BD
BD
其中正确的结论有( ).
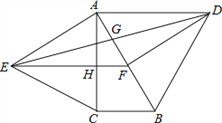
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
参考答案:
【答案】C
【解析】∵△ACE是等边三角形,∴∠EAC=60°,AE=AC.
∵∠BAC=30°,∴∠FAE=∠ACB=90°,AB=2BC.
∵F为AB的中点,∴AB=2AF,∴BC=AF,∴△ABC≌△EFA,∴FE=AB,
∴∠AEF=∠BAC=30°,∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,∴HF∥BC.
∵F是AB的中点, ![]() .
.
![]() ,AB=BD,
,AB=BD, ![]() ,故④说法正确;
,故④说法正确;
∵AD=BD,BF=AF,∴∠DFB=90°,∠BDF=30°.
∵∠FAE=∠BAC+∠CAE=90°,∴∠DFB=∠EAF.
∵EF⊥AC,∴∠AEF=30°,∴∠BDF=∠AEF,∴△DBF≌△EFA(AAS),∴AE=DF.
∵FE=AB,∴四边形ADFE为平行四边形.
∵AE≠EF,∴四边形ADFE不是菱形;故②说法不正确;
∵四边形ADFE为平行四边形,
![]() ,
, ![]() .
.
∵AD=AB,∴AD=4AG,故③说法正确,
所以正确的有:①③④.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=
 ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D

(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过抛物线y=
 x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长
 (单位长度)。慢车长
(单位长度)。慢车长 (单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点
(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点 为原点,取向右方向为正方向画数轴,此时快车
为原点,取向右方向为正方向画数轴,此时快车 在数轴上表示的数是
在数轴上表示的数是 ,慢车头
,慢车头 在数轴上表示的数是
在数轴上表示的数是 ,若快车
,若快车 以
以 个单位长度/秒的速度向右匀速继续行驶,同时慢车
个单位长度/秒的速度向右匀速继续行驶,同时慢车 以
以 个单位长度/秒的速度向左匀速继续行驶,且
个单位长度/秒的速度向左匀速继续行驶,且 与
与 互为相反数.
互为相反数.(1)求此时刻快车头
 与慢车头
与慢车头 之间相距多少单位长度?
之间相距多少单位长度?(2)从此时刻开始算起,问再行驶多少秒两列火车行驶到车头
 、
、 相距
相距 个单位长度?
个单位长度?(3)此时在快车
 上有一位爱到脑筋的七年级学生乘客
上有一位爱到脑筋的七年级学生乘客 ,他发现行驶中有一段时间,他的位置
,他发现行驶中有一段时间,他的位置 到两列火车头
到两列火车头 、
、 的距离和加上到两列火车尾
的距离和加上到两列火车尾 、
、 的距离和是一个不变的值(即
的距离和是一个不变的值(即 为定值),你认为学生
为定值),你认为学生 发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.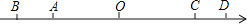
附加题:
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数
60≤x<90
90≤x<120
120≤x<150
150≤x<180
180≤x<210
频数
16
25
9
7
3
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几(精确到0.1%)?
相关试题

