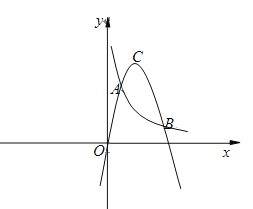
[题目]函数图象有一个公共点.我们就称两个函数图象“共一点 .有两个公共点.则称它们“共两点 (1)若函数y＝-x+b图像和y＝-x2+2x图像“共一点 P.求P点坐标,(2)若函数y＝-x+1图像和y＝ax2+2x图像“共两点 .则a的取值范围是: ,(3)若函数y＝与y＝ax2+bx图像在第一象限“共两点 A.B.且A.B两点之间水平� 题目和参考答案——青夏教育精英家教网—

【题目】函数图象有一个公共点，我们就称两个函数图象“共一点”，有两个公共点，则称它们“共两点”

（1）若函数y＝－x＋b图像和y＝－x2＋2x图像“共一点”P，求P点坐标；

（2）若函数y＝－x＋1图像和y＝ax2＋2x图像“共两点”，则a的取值范围是：；

（3）若函数y＝与y＝ax2＋bx图像在第一象限“共两点”A、B（A在B左侧），且A、B两点之间水平距离为2，两点之间垂直距离是A到y轴距离的倒数，设函数y＝ax2＋bx图像的顶点为C．求顶点C的坐标

【答案】(1)、()；(2)、a＞－，且a≠0；(3)、C为（，）

【解析】

试题分析：(1)、首先列出一元二次方程，根据方程有一个解得出b的值，然后计算交点坐标；(2)、根据方程有两个不相等的实数根，得出a的取值范围；(3)、设A点的横坐标为m，则B点的横坐标为m+2，根据点在反比例函数图象上得出A、B两点的坐标，根据距离求出m的值，然后将A、B两点的坐标代入二次函数解析式，求出a、b的值，从而得到函数的顶点坐标.

试题解析：(1)、∵函数y＝－x＋b图像和y＝－＋2x图像“共一点”，

∴－x＋b＝－＋2x，且b2－4ac=9－4b=0 ∴b=

当b=时，y＝－x＋，－x＋＝－＋2x．解得x＝，把x＝代入y＝－x＋中，得y＝．

∴P坐标为（）．

(2)、a＞－，且a≠0．

(3)、设A的横坐标为m，则B的横坐标为m＋2，∵A、B在y=图像上，

∴A、B分别表示为（m，），（m＋2，）． ∵两点之间垂直距离是A到y轴距离的倒数，

∴－=.解得m＝2，经检验，m＝2是原方程的根．当m＝2时，A、B分别为（2，1），（4，），

∵A、B在函数y＝a＋bx图像上，

∴1=4a＋2b，=16a＋4b．解得a=－，b=．

∴y＝－＋x，其顶点坐标C为（，）．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>