Question

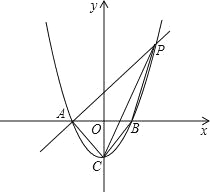
【题目】如图，在直角坐标系中，O为坐标原点，二次函数y=x2+mx+2的图象与x轴的正半轴交于点A，与y轴的正半轴交交于点B，且OA：OB=1：2．设此二次函数图象的顶点为D．

（1）求这个二次函数的解析式；

（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置．将上述二次函数图象沿y轴向上或向下平移后经过点C．请直接写出点C的坐标和平移后所得图象的函数解析式；

（3）设（2）中平移后所得二次函数图象与y轴的交点为B1，顶点为D1．点P在平移后的二次函数图象上，且满足△PBB1的面积是△PDD1面积的2倍，求点P的坐标．

Answer 1

【答案】

【解析】

试题分析：（1）先求出A、B两点坐标，利用待定系数法即可解决问题．

（2）如图1中，由题意可知，C（3，1），作CG∥OB交抛物线于G．x=3时，y=2，推出点G坐标（3，2），所以把抛物线向下平移1个单位即可经过点C，由此即可解决问题．

（3）如图2中，设P（m，m2﹣3m+1），由题意BB1=DD1，△PBB1的面积是△PDD1面积的2倍，可得m=2|﹣m|，解方程即可．

试题解析：（1）∵二次函数y=x2+mx+2的图象与x轴的正半轴交于点A，与y轴的正半轴交交于点B，且OA：OB=1：2，∴B（0，2），A（1，0），把A（1，0）代入y=x2+mx+2得m=﹣3，

∴二次函数的解析式为y=x2﹣3x+2．

（2）如图1中，

由题意可知，C（3，1），作CG∥OB交抛物线于G．x=3时，y=2，

∴点G坐标（3，2），∴把抛物线向下平移1个单位即可经过点C，

∴平移后的抛物线的解析式为y=x2﹣3x+1．

（3）如图2中，设P（m，m2﹣3m+1），

∵BB1=DD1，△PBB1的面积是△PDD1面积的2倍，∴m=2|﹣m|，

∴m=1或3，∴点P坐标为（1，﹣1）或（3，1）．