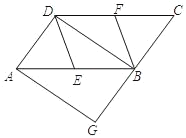
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
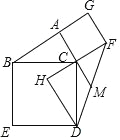
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先判断出∠ACB=∠HCD,即可得出结论;(2)先求出△ABC 的面积,进而求出 S△HDC=S△ABC=![]() ,进而得出 S△DHF=2S△CDH=
,进而得出 S△DHF=2S△CDH= ![]() ,再判断出△FCM∽△FHD,即可得出结论.
,再判断出△FCM∽△FHD,即可得出结论.
(1)∵四边形 BCDE 是正方形,
∴BC=CD,∠BCD=90°,
∵四边形 ACFG 是正方形,
∴CF=AG=AC,∠ACF=∠ACH=90°,
∴∠ACB=∠HCD,
∵DH⊥CF,
∴∠H=90°=∠BAC,
在△ABC 和△HDC 中, ,
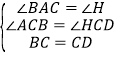 ,
,
∴△ABC≌△HDC;
(2)∵AG= ![]() ,
,
∴AC=![]() ,
,
在 Rt△ABC 中,tan∠ABC=![]() ,
,
∴AB= ![]() AC=
AC= ![]() ,
,
∴S△ABC= ![]() AB×AC=
AB×AC= ![]() ,
,
∵△ABC≌△HDC,
∴S△HDC=S△ABC=![]() ,AC=CH,
,AC=CH,
∴CH=CF,
∴S△DHF=2S△CDH=![]() ,
,
∵∠FCM=∠H=90°,
∴CM∥HD,
∴△FCM∽△FHD,
∴![]() ,
,
∴S△FCM= ![]() S△FHD=
S△FHD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O 是△ABC 的外接圆,BC 是直径,AC=2DH,过点 D 作 DH 垂直BC 于点 H,以下结论中:①BH=HD;②∠BAO=∠BOD;③
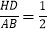 ;④连接 AO、BD,若 BC=8,sin∠HDO=
;④连接 AO、BD,若 BC=8,sin∠HDO=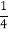 ,则四边形 ABDO 的面积为
,则四边形 ABDO 的面积为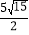 , 其中正确的结论是 ____(请填写序号)
, 其中正确的结论是 ____(请填写序号)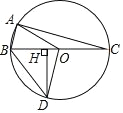
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=
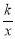 (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级
中位数(分)
众数(分)
平均数(分)
一班
85
二班
100
85
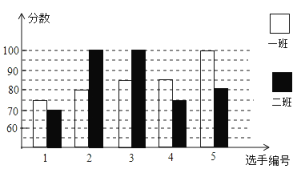
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,AD=4,AB=8,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,求四边形AGBD的面积.
相关试题

