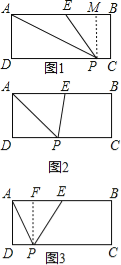
【题目】矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP=_____________.
参考答案:
【答案】1或4或9.
【解析】试题首先根据题意画出图形,共分3种情况,画出图形后根据勾股定理即可算出DP的长.
解:(1)如图1,当AE=EP=5时,
过P作PM⊥AB,
∴∠PMB=90°,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴四边形BCPM是矩形,
∴PM=BC=3,
∵PE=5,
∴EM=![]() =
=![]() =4,
=4,
∵E是AB中点,
∴BE=5,
∴BM=PC=5﹣4=1,
∴DP=10﹣1=9;
(2)如图2,当AE=AP=5时,DP=![]() =
=![]() =4;
=4;
(3)如图3,当AE=EP=5时,
过P作PF⊥AB,
∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,
∴四边形BCPF是矩形,
∴PF=AD=3,
∵PE=5,
∴EF=![]() =4,
=4,
∵E是AB中点,
∴AE=5,
∴DP=AF=5﹣4=1.
故答案为:1或4或9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线1上依次摆放着四个正方形和三个等腰直角三角形(阴影图形),已知三个等腰直角三角形的面积从左到右分别为1、2、3,四个正方形的面积从左到右依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )

A. 4 B. 5 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A, B两点,分别表示的数为
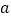 ,
, ,且
,且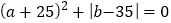 .点P从A点出发以每秒13个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒2个单位长度向左匀速运动,当点Q达到A点时,点P,Q停止运动.
.点P从A点出发以每秒13个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒2个单位长度向左匀速运动,当点Q达到A点时,点P,Q停止运动.(1)填空:
 ,
,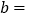 ;
;(2)求运动了多长时间后,点P,Q第一次相遇,以及相遇点所表示的数;
(3)求当点P,Q停止运动时,点P所在的位置表示的数;
(4)在整个运动过程中,点P和点Q一共相遇了几次.(直接写出答案)


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE= .
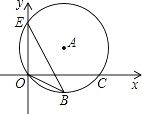
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理过程:
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
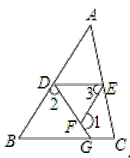
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

相关试题

