【题目】在Rt△ABC中,BC=AC,∠ACB=90°,D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE,BF.
(1)当点D在线段AB上时(点D不与点A,B重合),如图23(a).
①请你将图形补充完整;
②线段BF,AD所在直线的位置关系为________,线段BF,AD的数量关系为________.
(2)当点D在线段AB的延长线上时,如图23(b).
在(1)中②问的结论是否仍然成立?如果成立,请进行证明;如果不成立,请说明理由.

参考答案:
【答案】(1)①见解析;②垂直,相等;(2)成立,理由见解析.
【解析】
(1)①如图所示.

②根据CD⊥EF,可得∠DCF=90°.由于∠ACB=90°,可得∠ACB=∠DCF,∠ACD=∠BCF.
根据AC=BC,CD=CF,可判定△ACD≌△BCF,根据全等三角形的性质可得AD=BF,∠BAC=∠FBC,继而可得∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
(2)根据CD⊥EF,可得∠DCF=90°,由于∠ACB=90°,可证∠DCF=∠ACB,
所以∠DCF+∠BCD=∠ACB+∠BCD,继而可得∠BCF=∠ACD,根据AC=BC,CD=CF,
可判定△ACD≌△BCF,根据全等三角形的性质可得AD=BF,∠BAC=∠FBC,所以∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
解:(1)①如图所示.

②∵CD⊥EF,
∴∠DCF=90°.
∵∠ACB=90°,
∴∠ACB=∠DCF,
∴∠ACD=∠BCF.
又∵AC=BC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
故答案为:垂直,相等.
(2)成立.
证明:∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠DCF=∠ACB,
∴∠DCF+∠BCD=∠ACB+∠BCD,
∴∠BCF=∠ACD,
又∵AC=BC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,即BF⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2﹣4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为 .
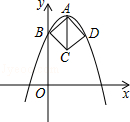
-
科目: 来源: 题型:
查看答案和解析>>【题目】三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点.
(1)求线段CM的长;
(2)求线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图24①,点A,B,C,D在同一直线上,AB=CD,作EC⊥AD于点C,FB⊥AD于点B,且AE=DF.
(1)求证:EF平分线段BC;
(2)若将△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.
相关试题

