Question

【题目】如图24①，点A，B，C，D在同一直线上，AB＝CD，作EC⊥AD于点C，FB⊥AD于点B，且AE＝DF.

(1)求证：EF平分线段BC；

(2)若将△BFD沿AD方向平移得到图②时，其他条件不变，(1)中的结论是否仍成立？请说明理由．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

(1)现根据CE⊥AD,BF⊥AD,可得∠ACE=∠DBF=90°,由于AB=CD,

所以AB+BC=BC+CD,即AC=DB,在Rt△ACE和Rt△DBF中,

,可证Rt△ACE≌Rt△DBF,继而可得CE=FB,

在Rt△CEG和Rt△BFG中,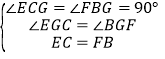,可证Rt△CEG≌Rt△BFG,

可得CG=BG,即EF平分线段BC.

(2)先根据CE⊥AD,BF⊥AD,可得∠ACE=∠DBF=90°,由于AB=CD,可得AB-BC=CD-BC,即AC=DB,在Rt△ACE和Rt△DBF中,,可证Rt△ACE≌Rt△DBF,可得CE=FB,

在Rt△CEG和Rt△BFG中,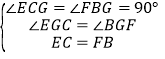,可证Rt△CEG≌Rt△BFG,

可得CG=BG,即EF平分线段BC.

(1)因为CE⊥AD,BF⊥AD,

所以∠ACE=∠DBF=90°,

因为AB=CD,

所以AB+BC=BC+CD,即AC=DB,

在Rt△ACE和Rt△DBF中,

,

所以Rt△ACE≌Rt△DBF,

所以CE=FB,

在Rt△CEG和Rt△BFG中,

,

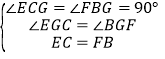所以Rt△CEG≌Rt△BFG,

所以CG=BG,即EF平分线段BC.

(2)(1)中结论成立,理由为:

因为CE⊥AD,BF⊥AD,

所以∠ACE=∠DBF=90°,

因为AB=CD,

所以AB-BC=CD-BC,即AC=DB,

在Rt△ACE和Rt△DBF中,

,

所以Rt△ACE≌Rt△DBF,

所以CE=FB,

在Rt△CEG和Rt△BFG中,

,

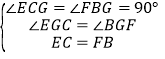所以Rt△CEG≌Rt△BFG,

所以CG=BG,即EF平分线段BC.