Question

【题目】如图，已知点A(-2，4)和点B(1，0)都在抛物线上．

（1）求、；

（2）向右平移上述抛物线，记平移后点A的对应点为，点B的对应点为，若四边形为菱形，求平移后抛物线的表达式；

（3）记平移后抛物线的对称轴与直线的交点为C，试在轴上找一个点D，使得以点、C、D为顶点的三角形与△ABC相似.

Answer 1

【答案】（1）；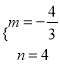

（2）；.

（3）D点坐标为：D（3，0）或（，0）

【解析】（1）已知了抛物线图象上A、B两点的坐标，将它们代入抛物线的解析式中，即可求得m、n的值；（2）根据A、B的坐标，易求得AB的长；根据平移的性质知：四边形AA′B′B一定为平行四边形，若四边形AA′B′B为菱形，那么必须满足AB=BB′，由此可确定平移的距离，根据“左加右减”的平移规律即可求得平移后的抛物线解析式；（3）易求得直线AB′的解析式，联立平移后的抛物线对称轴，可得到C点的坐标，进而可求出AB、BC、AC、B′C的长，在（2）题中已经证得AB=BB′，那么∠BAC=∠BB′C，即A、B′对应，若以点B′、C、D为顶点的三角形与△ABC相似，可分两种情况考虑：①∠B′CD=∠ABC，此时△B′CD∽△ABC，②∠B′DC=∠ABC，此时△B′DC∽△ABC，根据上述两种不同的相似三角形所得不同的比例线段，即可求得不同的BD长，进而可求得D点的坐标．

解：（1）由于抛物线经过点A（-2，4）和点B（1，0），

则有： ，解得.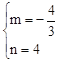

（2）由（1）得：，

由A（-2，4）、B（1，0），根据勾股定理可得，

若四边形AA′B′B为菱形，则AB=BB′=5，即B′（6，0）.

故抛物线需向右平移5个单位，即：.

（3）依照题意画出图形，如图所示，

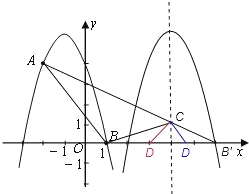
由（2）得：平移后抛物线的对称轴为：x=4，

∵A（2，4），B′（6，0），∴直线AB′：.

当x=4时，y=1，故C（4，1）. ∴B′C=，AC=3，BC=.

由（2）知：AB=BB′=5，即∠BAC=∠BB′C.

若以点B′、C、D为顶点的三角形与△ABC相似，

则：①∠B′CD=∠ABC，则△B′CD∽△ABC，可得：，即，∴B′D=3，此时D（3，0）；

②∠B′DC=∠ABC，则△B′DC∽△ABC，可得：即，∴，此时D（，0）.

综上所述，存在符合条件的D点，且坐标为：D（3，0）或（，0）．

“点睛”本题考查了二次函数综合题、平移问题、曲线上点的坐标与方程的关系、勾股定理、菱形的性质、等腰三角形的性质、相似三角形的判定和性质；本题主要考查了二次函数的应用问题，在解题时要根据二次函数的图象和性质进行综合分析是本题的关键．要注意分类思想的应用．