【题目】如图，已知：在△ABC中，∠ACB＝90°，CD为高，且CD、CE三等分∠ACB.

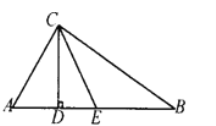
（1）求∠B的度数.

（2）求证：CE是AB边上的中线，且．

参考答案：

【答案】（1）∠ B=；（2）证明见解析.

【解析】分析：(1)利用直角△BCD的两个锐角互余的性质进行解答;(2)利用已知条件和(1)中的结论可以得到△ACE是等边三角形和△BCE为等腰三角形,利用等腰三角形的性质证得结论.

本题解析：(1)∵在△ABC中,∠ACB=90°，CD，CE三等分∠ACB，

∴∠ACD=∠DCE=∠BCE=30°,则∠BCD=60°，又∵CD为高，∴∠B=90°60°=30°；

(2)证明：由(1)知,∠B=∠BCE=30°,则CE=BE,AC=AB.

∵∠ACB=90°,∠B=30°，∴∠A=60°，又∵由(1)知,∠ACD=∠DCE=30°，

∴∠ACE=∠A=60°，∴△ACE是等边三角形，∴AC=AE=EC=AB，

∴AE=BE，即点E是AB的中点。∴CE是AB边上的中线,且CE=AB.

关闭