【题目】为方便市民出行,减轻城市中心交通压力,佛山市掀起新一轮城市基础设施建设高潮,动工修建贯穿东西、南北的地铁2、3号线,已知修建地铁2号线32千米和3号线66千米共投资581.6亿元;且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元.
(1)求2号线、3号线每千米的平均造价分别是多少亿元?
(2)除地铁1、2、3号线外,佛山市政府规划未来五年,还要再建108千米的地铁线网.据预算,这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍,则还需投资多少亿元?
参考答案:
【答案】(1)2号线每千米的平均造价是5.8亿元,3号线每千米的平均造价是6亿元;(2)还需投资1209.6亿元.
【解析】试题分析:(1)设2号线每千米的平均造价是x亿元,3号线每千米的平均造价是y亿元,根据题意列出方程组解答即可;
(2)根据(1)中求解所求,得出建168千米的地铁线网,每千米的造价,进而求出即可.
试题解析:(1)设2号线每千米的平均造价是x亿元,3号线每千米的平均造价是y亿元,
由题意得出: ![]() ,
,
解得: ![]() ,
,
答:2号线每千米的平均造价是5.8亿元,3号线每千米的平均造价是6亿元;
(2)由(1)得出:
168×6×1.2=1209.6(亿元),
答:还需投资1209.6亿元.
-
科目: 来源: 题型:
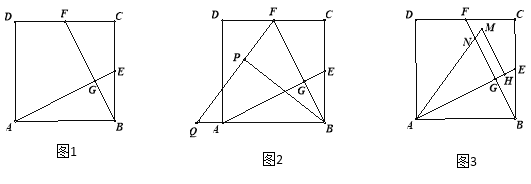
查看答案和解析>>【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地计划用120﹣180天(含120和180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石比原计划多5000米3,工期比原计划减少了24天,则原计划和实际平均每天运送土石方各是多少万米3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:3x﹣5≤2(x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=
 ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

-
科目: 来源: 题型:
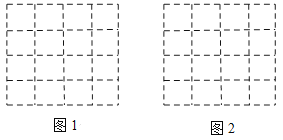
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形:
(1)使三角形的三边长分别为
 (在图1中画一个即可);
(在图1中画一个即可);(2)使三角形为钝角三角形且面积为4(在图2中画一个即可)。
相关试题

