【题目】如图,在![]() 中,∠ABC的平分线与∠ACE平分线相交于点D,
中,∠ABC的平分线与∠ACE平分线相交于点D,![]() .求∠BAD的度数.
.求∠BAD的度数.

参考答案:
【答案】110°
【解析】
根据三角形外角的性质,可得∠BDC=![]() ∠BAC,过D点分别作DE⊥BE交于E点,DG⊥AC交于G点,DF⊥BF交BA的延长线于F点,易证Rt△DGA≌Rt△DFA,从而得∠DAG=∠DAF,进而即可求解.
∠BAC,过D点分别作DE⊥BE交于E点,DG⊥AC交于G点,DF⊥BF交BA的延长线于F点,易证Rt△DGA≌Rt△DFA,从而得∠DAG=∠DAF,进而即可求解.
∵∠ABC的平分线BM与△ACB的外角∠ACE的平分线CD相交于点D,
∴∠DCE= ∠ACE,∠DBC= ∠ABC,
∵∠DCE是△BCD的外角,
∴∠BDC=∠DCE-∠DBC= ![]() ∠ACE-
∠ACE- ![]() ∠ABC=
∠ABC= ![]() (∠BAC+∠ABC)-
(∠BAC+∠ABC)-![]() ∠ABC=
∠ABC= ![]() (∠BAC+ ∠ABC- ∠ABC)=
(∠BAC+ ∠ABC- ∠ABC)= ![]() ∠BAC,
∠BAC,
∵∠BDC=20°,
∴∠BAC=2×20°=40°,
过D点分别作DE⊥BE交于E点,DG⊥AC交于G点,DF⊥BF交BA的延长线于F点,
∵BD平分∠ABC,CD平分∠ACE,
∴DE=DF,DE=DG,
∴DF =DG;
在Rt△DGA与Rt△DFA中,
∵DF =DG,DA=DA,
∴Rt△DGA≌Rt△DFA(HL),
∴∠DAG=∠DAF,
又∵∠BAC=40°,
∴∠CAF=140°,
∴∠CAD=70°,
∴∠BAD=∠BAC+∠CAD =110°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;
(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;
(3)如图3,若
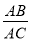 =a,且
=a,且 =b,直接写出
=b,直接写出 = .
= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D在反比例函数y=
 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= .
.(1)求反比例函数y=
 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为
 ,瓶中水面的高度为
,瓶中水面的高度为 ,下面能大致表示上面故事情节的图象是( )
,下面能大致表示上面故事情节的图象是( ) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(m,0),点B的坐标为(m﹣2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据
 ≈1.41,
≈1.41,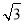 ≈1.73.
≈1.73.
相关试题

