【题目】如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.

参考答案:
【答案】(1)y=﹣![]() ,y=
,y=![]() x﹣2;(2)AC=CD, AC⊥CD,理由见解析;(3)45°.
x﹣2;(2)AC=CD, AC⊥CD,理由见解析;(3)45°.
【解析】分析:(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;
(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD;(3)连接AD,可证得四边形AEBD为平行四边形,可得出△ACD为等腰直角三角形,则可求得答案.
本题解析:
(1)∵A(5,0),∴OA=5.∵tan∠OAC=![]() ,∴
,∴![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),∴BD=OC=2,∵B(0,3),BD∥x轴,∴D(﹣2,3),
∴m=﹣2×3=﹣6,∴y=﹣![]() ,
,
设直线AC关系式为y=kx+b,∵过A(5,0),C(0,﹣2),
∴![]() ,解得
,解得 ,∴y=
,∴y=![]() x﹣2;
x﹣2;
(2)∵B(0,3),C(0,﹣2),∴BC=5=OA,
在△OAC和△BCD中
 ,∴△OAC≌△BCD(SAS),∴AC=CD,
,∴△OAC≌△BCD(SAS),∴AC=CD,
∴∠OAC=∠BCD,∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,

∵AE=OC,BD=OC,AE=BD,∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,∴∠BMC=∠DAC,
∵△OAC≌△BCD,∴AC=CD,
∵AC⊥CD,∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y﹣3与x成正比例,并且当x=2时,y=7;
(1)求y与x之间的函数关系式;
(2)当x=5时,y的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=_____,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,点D,E在⊙O上,连接AE,DE,CD,BE,CE,∠EAC+∠BAE=180°,
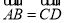 .
.(1)判断BE与CE之间的数量关系,并说明理由;
(2)求证:△ABE≌△DCE;
(3)若∠EAC=60°,BC=8,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=3,a2+b2=5,则ab的值为( )
A. ﹣2 B. ﹣1 C. 1 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形的两边长分别为 2cm 和 4cm,且第三条边为偶数,那么这个三角形的周长为______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年来全国各省市政府民生实事之一的公共自行车建设工作已基本完成,网上资料显示呼和浩特市某部门对2017年4月份中的7天进行了公共自行车日
租量的统计,结果如图:

(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)该市共租车多少万车次;
(3)资料显示,呼市政府在公共自行车建设项目中共投入9600万元,估计2017年共租车3200万车次,每车次平均收入租车费0.1元,求2017年该市租车费收入占总投入的百分率(精确到0.1%).
相关试题

