【题目】如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB=a,且BD=BE.
(1)求证:AC=AD+CE;
(2)若a=120°,点F在直线l的上方,△BEF为等边三角形,补全图形,请判断△ACF的形状,并说明理由.

参考答案:
【答案】(1)详见解析;(2)△ACF为等边三角形.
【解析】
(1)由外角的性质可得∠ADB=∠CBE,由“AAS”可得△ADB≌△CBE,可得AD=CB,AB=CE,可得结论;
(2)由“SAS”可证△AFB≌△CFE,可得AF=CF,∠AFB=∠CFE,可得∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°,可得△ACF是等边三角形.
证明:(1)∵∠DAB=∠DBE=α,
∴∠ADB+∠ABD=∠CBE+∠ABD=180°﹣α.
∴∠ADB=∠CBE
在△ADB和△CBE中,
∵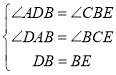 ,
,
∴△ADB≌△CBE(AAS)
∴AD=CB,AB=CE.
∴AC=AB+BC=AD+CE
(2)补全图形.
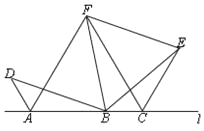
△ACF为等边三角形.
理由如下:
∵△BEF为等边三角形,
∴BF=EF,∠BFE=∠FBE=∠FEB=60°.
∵∠DBE=120°,∴∠DBF=60°.
∵∠ABD=∠CEB(已证),
∴∠ABD+∠DBF=∠CEB+∠FEB,
即∠ABF=∠CEF.
∵AB=CE(已证),
∴△AFB≌△CFE(SAS),
∴AF=CF,∠AFB=∠CFE.
∴∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°.
∴△ACF为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料,两次购买饲料价格分别为m元/千克和n元/千克,且m≠n,两名采购员的采购方式也不同,其中甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?(用字母m、n表示)
(2)谁的购货方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
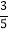 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx+n与反比例函数y=
 其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”.
例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.

(1)如图1,在△ABC中,D是边BC上一点,若∠B=30°,∠BAD=∠C=40°,求证: AD为△ABC的“等角分割线”;
(2)如图2,△ABC中,∠C=90°,∠B=30°;
①画出△ABC的“等角分割线”,写出画法并说明理由;
②若BC=3,求出①中画出的“等角分割线”的长度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割线”CD,直接写出所有符合要求的∠B的度数.
相关试题

