【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
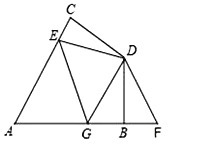
(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明).
参考答案:
【答案】(1)证明见解析;
(2)CE、EG、BG之间的数量关系为:CE+BG=EG,证明见解析;
(3)当∠EDG=90°﹣![]() α时, CE+BG=EG仍然成立.
α时, CE+BG=EG仍然成立.
【解析】试题分析:(1)首先判断出∠C=∠DBF,然后根据全等三角形判定的方法,判断出△CDE≌△BDF,即可判断出DE=DF.(2)猜想CE、EG、BG之间的数量关系为:CE+BG=EG.首先根据全等三角形判定的方法,判断出△ABD≌△ACD,即可判断出∠BDA=∠CDA=60°;然后根据∠EDG=60°,可得∠CDE=∠ADG,∠ADE=∠BDG,再根据∠CDE=∠BDF,判断出∠EDG=∠FDG,据此推得△DEG≌△DFG,所以EG=FG,最后根据CE=BF,判断出CE+BG=EG即可.(3)根据(2)的证明过程,要使CE+BG=EG仍然成立,则∠EDG=∠BDA=∠CDA=![]() ∠CDB,即∠EDG=
∠CDB,即∠EDG=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,据此解答即可.
α,据此解答即可.
试题解析:(1):∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°﹣60°﹣120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在△CDE和△BDF中,
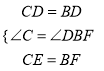 (SAS)
(SAS)
∴△CDE≌△BDF,
∴DE=DF.
(2)解:如图1,连接AD,猜想CE、EG、BG之间的数量关系为:CE+BG=EG.
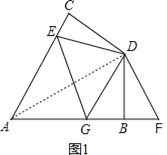
证明:在△ABD和△ACD中,
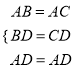 (SSS)
(SSS)
∴△ABD≌△ACD,
∴∠BDA=∠CDA=![]() ∠CDB=
∠CDB=![]() ×120°=60°,
×120°=60°,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得△CDE≌△BDF,
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在△DEG和△DFG中,
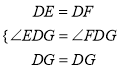
∴△DEG≌△DFG,
∴EG=FG,
又∵CE=BF,FG=BF+BG,
∴CE+BG=EG;
(3)解:要使CE+BG=EG仍然成立,
则∠EDG=∠BDA=∠CDA=![]() ∠CDB,
∠CDB,
即∠EDG=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴当∠EDG=90°﹣![]() α时, CE+BG=EG仍然成立.
α时, CE+BG=EG仍然成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把6800000,用科学记数法表示为( )
A. 6.8×105 B. 6.8×106 C. 6.8×107 D. 6.8×108
-
科目: 来源: 题型:
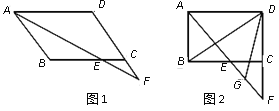
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交直线BC于E,交直线DC于F。
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),讨论线段DG与BD的数量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,解答后面提出的问题:
黑白双雄,纵横江湖;双剑合壁,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:(2+
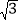 )(2-
)(2-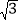 )=1,(
)=1,(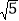 +
+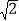 )(
)(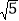 -
-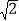 )=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
)=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解: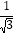 =
=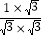 =
= ,
,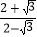 =
=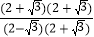 =7+4
=7+4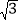 .像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:
(1)4+
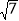 的有理化因式是 ,将
的有理化因式是 ,将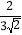 分母有理化得 ;
分母有理化得 ;(2)已知x=
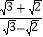 ,y=
,y=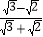 ,则
,则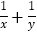 = ;
= ;(3)已知实数x,y满足(x+
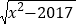 )(y+
)(y+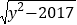 )-2017=0,则x= ,y= .
)-2017=0,则x= ,y= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据5,7,2,5,6的中位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数3和12的比例中项是 .
相关试题

