【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
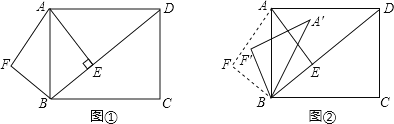
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角(锐角),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
参考答案:
【答案】(1)4,3;(2)3,![]() .(3)
.(3)![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
试题分析:(1)利用矩形性质、勾股定理及三角形面积公式求解;
(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;
(3)在旋转过程中,等腰△DPQ有4种情形,如答图3所示,对于各种情形分别进行计算.
试题解析:(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=![]() .
.
∵S△ABD=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE= .
.
在Rt△ABE中,AB=5,AE=4,由勾股定理得:BE=3.
(2)设平移中的三角形为△A′B′F′,如图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.

①当点F′落在AB上时,
∵AB∥A′B′,
∴∠3=∠4,
∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,
∴∠6=∠2,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,
∴B′D=B′F′=3,
∴BB′=BD-B′D=![]() ,即m=
,即m=![]() .
.
(3)存在.理由如下:
在旋转过程中,等腰△DPQ依次有以下4种情形:
①如答图3-1所示,点Q落在BD延长线上,且PD=DQ,易知∠2=2∠Q,
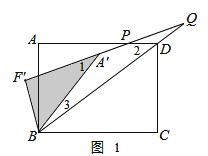
∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′B=5,
∴F′Q=F′A′+A′Q=4+5=9.
在Rt△BF′Q中,由勾股定理得:BQ=![]() .
.
∴DQ=BQ-BD=![]() ;
;
②如图3-2所示,点Q落在BD上,且PQ=DQ,易知∠2=∠P,

∵∠1=∠2,
∴∠1=∠P,
∴BA′∥PD,则此时点A′落在BC边上.
∵∠3=∠2,
∴∠3=∠1,
∴BQ=A′Q,
∴F′Q=F′A′-A′Q=4-BQ.
在Rt△BQF′中,由勾股定理得:BF′2+F′Q2=BQ2,
即:32+(4-BQ)2=BQ2,
解得:BQ=![]() ,
,
∴DQ=BD-BQ=![]() ;
;
③如图3-3所示,点Q落在BD上,且PD=DQ,易知∠3=∠4.

∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°-![]() ∠2.
∠2.
∵∠1=∠2,
∴∠4=90°-![]() ∠1.
∠1.
∴∠A′QB=∠4=90°-![]() ∠1,
∠1,
∴∠A′BQ=180°-∠A′QB-∠1=90°-![]() ∠1,
∠1,
∴∠A′QB=∠A′BQ,
∴A′Q=A′B=5,
∴F′Q=A′Q-A′F′=5-4=1.
在Rt△BF′Q中,由勾股定理得:BQ=![]() ,
,
∴DQ=BD-BQ=![]() ;
;
④如图3-4所示,点Q落在BD上,且PQ=PD,易知∠2=∠3.

∵∠1=∠2,∠3=∠4,∠2=∠3,
∴∠1=∠4,
∴BQ=BA′=5,
∴DQ=BD-BQ=![]() .
.
综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形;
DQ的长度分别为![]() 、
、![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一粒大米的质量约为0.000021千克,这个数用科学记数法表示为( )
A. 0.21×10-4 B. 2.1×10-4 C. 2.1×10-5 D. 21×10-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=-x+4的图象经过点(a,2)则a=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区在一次九年级数学质量检测试题中,有一道分值为8分的解答题,所有考生的得分只有四种,即:0分,3分,5分,8分,老师为了解本题学生得分情况,从全区4500名考生试卷中随机抽取一部分,分析、整理本题学生得分情况并绘制了如下两幅不完整的统计图:
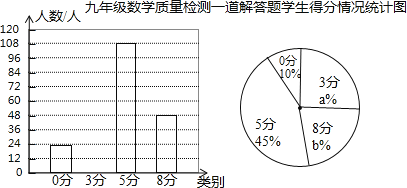
(1)本次调查从全区抽取了份学生试卷;扇形统计图中a= ,b= ;
(2)补全条形统计图;
(3)该地区这次九年级数学质量检测中,请估计全区考生这道8分解答题的平均得分是多少?得8分的有多少名考生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解扬州城区交通压力,城市南部快速通道已于4.18开工建设.某工程队承担了某道路900米长的改造任务.工程队在改造完360米道路后,引进了新设备,每天的工作效率比原来提高了20%,结果共用27天完成了任务,问引进新设备前工程队每天改造道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上的点A到原点的距离是3,则点A表示的是为( )
A. 6或﹣6 B. 3 C. ﹣3 D. 3或﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=1时,3ax2+bx的值为2,则当x=3时,ax2+bx的值_________.
相关试题

