【题目】如图正方形ABCD的边长为4,E、F分别为DC、BC中点.

(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
参考答案:
【答案】解:(1)证明:∵四边形ABCD为正方形,∴AB=AD,∠=90°,DC=CB,
∵E、F为DC、BC中点,∴DE=![]() DC,BF=
DC,BF=![]() BC。∴DE=BF。
BC。∴DE=BF。
∵在△ADE和△ABF中, 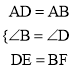 ,∴△ADE≌△ABF(SAS)。
,∴△ADE≌△ABF(SAS)。
(2)由题知△ABF、△ADE、△CEF均为直角三角形,
且AB=AD=4,DE=BF=![]() ×4=2,CE=CF=
×4=2,CE=CF=![]() ×4=2,
×4=2,
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF
=4×4﹣![]() ×4×2﹣
×4×2﹣![]() ×4×2﹣
×4×2﹣![]() ×2×2=6。
×2×2=6。
【解析】试题分析:(1)、根据正方形的性质以及中点得出DE=DF,结合正方形的性质得出△ADE和△ABF全等;(2)、利用正方形的面积减去三个直角三角形的面积得出△AEF的面积.
试题解析:(1)、∵四边形ABCD为正方形, ∴AB=AD,∠=90°,DC=CB, ∵E、F为DC、BC中点,
∴DE=![]() DC,BF=
DC,BF=![]() BC, ∴DE=BF, ∵在△ADE和△ABF中,
BC, ∴DE=BF, ∵在△ADE和△ABF中,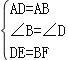 , ∴△ADE≌△ABF(SAS);
, ∴△ADE≌△ABF(SAS);
(2)、由题知△ABF、△ADE、△CEF均为直角三角形, 且AB=AD=4,DE=BF=![]() ×4=2,CE=CF=
×4=2,CE=CF=![]() ×4=2,
×4=2,
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF=4×4﹣![]() ×4×2﹣
×4×2﹣![]() ×4×2﹣
×4×2﹣![]() ×2×2=6.
×2×2=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y1=-x2+
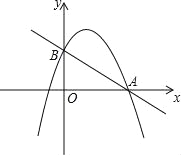
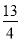 x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.
x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A. 点P在⊙O外 B. 点P在⊙O内 C. 点P在⊙O上 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=-a,|b|=b,|c|=-c,|d|=-d,a,b,c,d都不为零,并且|a|>|b|>|c|>|d|,请把a,b,c,d四个数从小到大用“<”号连结.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=
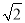 ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=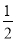 ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=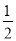 ,其中正确结论为( )
,其中正确结论为( )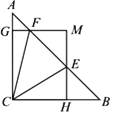
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面说法中正确的是 ( )
A. 两数之和为正,则两数均为正 B. 两数之和为负,则两数均为负
C. 两数之和为0,则这两数互为相反数 D. 两数之和一定大于每一个加数
相关试题

