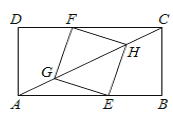
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是_________________。
参考答案:
【答案】![]()
【解析】
首先连接EF交AC于O,由矩形ABCD中,四边形EGFH是菱形,易证得△CFO≌△AOE(AAS),即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
连接EF交AC于O,
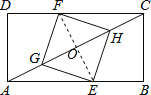
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
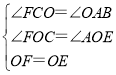 ,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=![]() ,
,
∴AO=![]() AC=5,
AC=5,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=
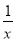 的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )A. y1<y2<y3B. y2<y3<y1C. y3<y2<y1D. y2<y1<y3
-
科目: 来源: 题型:
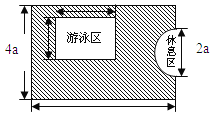
查看答案和解析>>【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
-
科目: 来源: 题型:
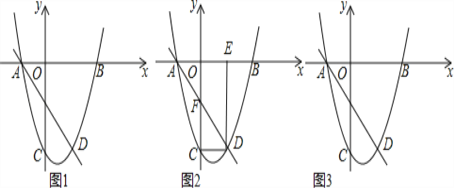
查看答案和解析>>【题目】如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
(1)求抛物线的解析式;
(2)如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4
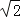 ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=
 ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
 B.
B.  +1﹣
+1﹣ C.
C.  ﹣
﹣ D.
D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
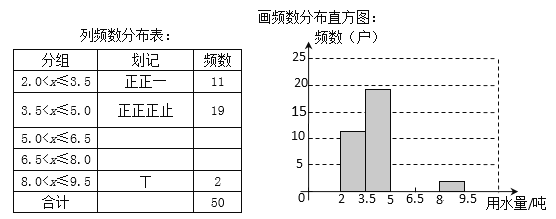
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
相关试题

