【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
参考答案:
【答案】![]()
【解析】解:延长EF和BC,交于点G
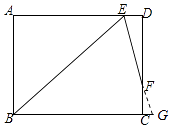
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE= ![]() =
= ![]() ,
,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE= ![]()
由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC
∴ ![]()
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴ ![]() =9+2x+x
=9+2x+x
解得x= ![]()
∴BC=9+2( ![]() ﹣3)=
﹣3)= ![]()
故答案为: ![]()
在矩形ABCD中,∠B的角平分线BE与AD交于点E,得到∠ABE=∠AEB=45°,AB=AE=9,直角三角形ABE中,BE= ![]() =
= ![]() ,又∠BED的角平分线EF与DC交于点F,得到∠BEG=∠DEF,由AD∥BC,得到∠G=∠DEF,∠BEG=∠G,BG=BE=
,又∠BED的角平分线EF与DC交于点F,得到∠BEG=∠DEF,由AD∥BC,得到∠G=∠DEF,∠BEG=∠G,BG=BE= ![]() ,由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC,得到
,由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC,得到 ![]() ,设CG=x,DE=2x,则AD=9+2x=BC,由BG=BC+CG,得到
,设CG=x,DE=2x,则AD=9+2x=BC,由BG=BC+CG,得到 ![]() =9+2x+x,解得x=
=9+2x+x,解得x= ![]() ,得到BC=9+2(
,得到BC=9+2( ![]() ﹣3)=
﹣3)= ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强
 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留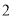 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早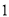 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程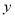 (千米)与行驶时间
(千米)与行驶时间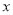 (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.(1)求点
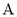 的纵坐标
的纵坐标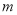 的值;
的值;(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间t(min)
1
2.5
5
10
20
50
…
路程s(km)
2
5
10
20
40
100
…
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶的路程为20 km时,所花的时间是多少分钟?
(3)随着t逐渐变大,s的变化趋势是什么?
(4)路程s与时间t之间的函数表达式为______________.
(5)按照这一行驶规律,当所花的时间t是300 min时,汽车行驶的路程s是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是
 .
.(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.

-
科目: 来源: 题型:
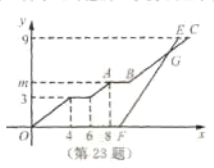
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
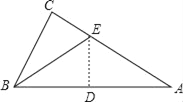
A. 2
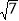 B.
B. 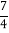 C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
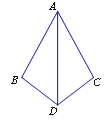
查看答案和解析>>【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
相关试题

