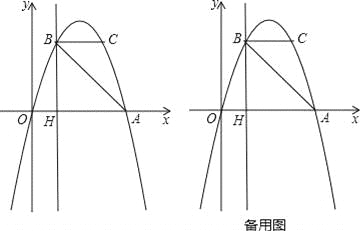
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
参考答案:
【答案】(1)y=﹣x2+4x;(2)(3,3);3;(3)(5,﹣5);(4)2.5或14.5或17或5
【解析】试题分析:(1)利用待定系数法求二次函数的表达式;(2)根据二次函数的对称轴x=2写出点C的坐标为(3,3),根据面积公式求△ABC的面积;(3)因为点P是抛物线上一动点,且位于第四象限,设出点P的坐标(m,﹣m2+4m),利用差表示△ABP的面积,列式计算求出m的值,写出点P的坐标;(4)分别以点C、M、N为直角顶点分三类进行讨论,利用全等三角形和勾股定理求CM或CN的长,利用面积公式进行计算.
试题解析:(1)把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,
得![]() 解得:
解得: ![]() ,
,
∴抛物线表达式为:y=﹣x2+4x;
(2)点C的坐标为(3,3),
又∵点B的坐标为(1,3),
∴BC=2,
∴S△ABC=![]() ×2×3=3;
×2×3=3;
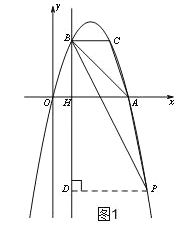
(3)过P点作PD⊥BH交BH于点D,
设点P(m,﹣m2+4m),
根据题意,得:BH=AH=3,HD=m2﹣4m,PD=m﹣1,
∴S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
6=![]() ×3×3+
×3×3+![]() (3+m﹣1)(m2﹣4m)﹣
(3+m﹣1)(m2﹣4m)﹣![]() (m﹣1)(3+m2﹣4m),
(m﹣1)(3+m2﹣4m),
∴3m2﹣15m=0,
m1=0(舍去),m2=5,
∴点P坐标为(5,﹣5).
(4)以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
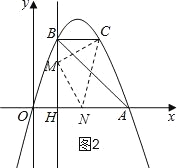
①以点M为直角顶点且M在x轴上方时,如图2,CM=MN,∠CMN=90°,
则△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴M(1,2),N(2,0),
由勾股定理得:MC=![]() ,
,
∴S△CMN=![]() ×
×![]() ×
×![]() =
=![]() ;
;
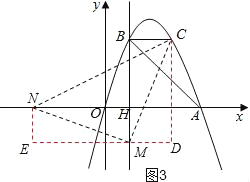
②以点M为直角顶点且M在x轴下方时,如图3,作辅助线,构建如图所示的两直角三角形:Rt△NEM和Rt△MDC,
得Rt△NEM≌Rt△MDC,
∴EM=CD=5,MD=ME=2,
由勾股定理得:CM=![]() =
=![]() ,
,
∴S△CMN=![]() ×
×![]() ×
×![]() =
=![]() ;
;
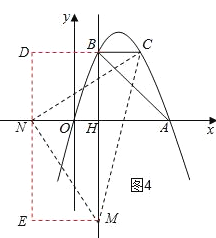
③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,作辅助线,
同理得:CN=![]() =
=![]() ,
,
∴S△CMN=![]() ×
×![]() ×
×![]() =17;
=17;
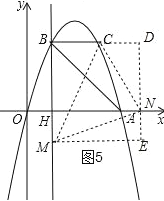
④以点N为直角顶点且N在y轴右侧时,作辅助线,如图5,同理得:CN=![]() =
=![]() ,
,
∴S△CMN=![]() ×
×![]() ×
×![]() =5;
=5;
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上所述:△CMN的面积为: ![]() 或
或![]() 或17或5.
或17或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:aa2=
-
科目: 来源: 题型:
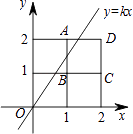
查看答案和解析>>【题目】将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
A.k≤2
B.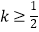
C.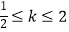
D.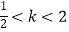
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省线的租车方案,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
-
科目: 来源: 题型:
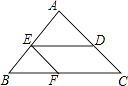
查看答案和解析>>【题目】如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,2,3,4,5的众数是_______.
相关试题

