【题目】做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的象与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;
③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是 ▲ (将正确结论的序号都填上).

参考答案:
【答案】![]()
【解析】分析:认真读题,由已知条件沿直线AD对折,重合,说明∠B与∠C相等,AD⊥BC,BD=CD,根据结论对号入座即可.
解答:解:从操作过程没有体现角相等,边就相等,故①不符合;
因为AB=AC,操作之后得到∠B与∠C重合,即等边对等角,故②符合;
根据所得的图象与△ACD重合,所以AD⊥BC,BD=CD,又AD平分∠BAC,所以③符合.
故操作可以得出的是②③两结论.
故填②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产,若购买3盒豆腐乳和2盒猕猴桃果汁共需60元;购买1盒豆腐乳和3盒猕猴桃果汁共需55元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )
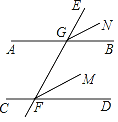
A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,请思考怎样把每个三角形纸片只剪一次,将它分成两个等腰三角形,试一试,在图中画出裁剪的痕迹.
(1)
 (2)
(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代对勾股定理有深刻的认识.
(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求(a+b)2的值;
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步
 =m;第二步:
=m;第二步:  =k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
=k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.

相关试题

