【题目】在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.

参考答案:
【答案】证明见试题解析,PE=PF,BE=CF,BF=CE.
【解析】试题分析:可证明△ABF≌△ACE,则BF=CE,再证明△BEP≌△CFP,则PB=PC,从而可得出PE=PF,BE=CF.
试题解析:在△ABF和△ACE中,∵AB=AC,∠BAF=∠CAE,AF=AE,
∴△ABF≌△ACE(SAS),∴∠ABF=∠ACE,∴BF=CE,
∵AB=AC,AE=AF,∴BE=CF,
在△BEP和△CFP中,∵∠BPE=∠CPF,∠PBE=∠PCF,BE=CF,∴△BEP≌△CFP(AAS),∴PB=PC,
∵BF=CE,∴PE=PF,∴图中相等的线段为PE=PF,BE=CF,BF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )
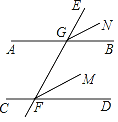
A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的象与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;
③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是 ▲ (将正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,请思考怎样把每个三角形纸片只剪一次,将它分成两个等腰三角形,试一试,在图中画出裁剪的痕迹.
(1)
 (2)
(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代对勾股定理有深刻的认识.
(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求(a+b)2的值;
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步
 =m;第二步:
=m;第二步:  =k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
=k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

相关试题

