【题目】我县某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从这两组中随机选取2名选手进行调研座谈,请用画树状图或列表法求第一组至少有1名选手被选中的概率.
参考答案:
【答案】(1)9;(2)162°;(3) ![]() .
.
【解析】分析:(1)根据被调查人数为20和表格中的数据可以求得a的值;
(2)根据表格中的数据可以得到分数在8≤m<9内所对应的扇形图的圆心角;
(3)根据题意可以写出所有的可能性,从而可以得到第一组至少有1名选手被选中的概率.
详解:(1)由题意可得:
a=20﹣2﹣7﹣2=9,即a的值是9;
(2)由题意可得:
分数在8≤m<9内所对应的扇形图的圆心角为:360°×![]() =162°;
=162°;
(3)由题意可得:所有的可能性如下图所示:
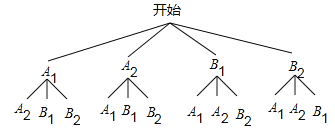
故第一组至少有1名选手被选中的概率是:![]() =
=![]() ,即第一组至少有1名选手被选中的概率是
,即第一组至少有1名选手被选中的概率是![]() .
.
-
科目: 来源: 题型:
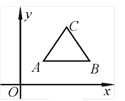
查看答案和解析>>【题目】如图,等边三角形ABC的顶点A、B坐标分别为(1,1)、(3,1),若把等边△ABC先沿x轴翻折,再向左平移1个单位”为第一次変换,则这样连续经过2017次变换后,等边△ABC的顶点C的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )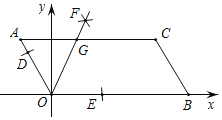
A. (
 ﹣1,2) B. (
﹣1,2) B. ( ,2) C. (3﹣
,2) C. (3﹣ ,2) D. (
,2) D. ( ﹣2,2)
﹣2,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4,表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:

若数轴上数-3表示的点与数1表示的点重合.(请依据此情境解决下列问题)
①则数轴上数3表示的点与数 表示的点重合.
②若点
 到与原点的距离是5个单位长度,并且
到与原点的距离是5个单位长度,并且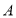 ,
,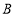 两点经折叠后重合,则点
两点经折叠后重合,则点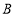 点表示的数是 .
点表示的数是 .③若数轴上
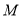 ,
,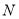 两点之间的距离为2018,并且
两点之间的距离为2018,并且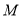 ,
,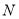 两点经折叠后重合,如果
两点经折叠后重合,如果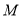 点表示的数比
点表示的数比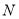 点表示的数大,则
点表示的数大,则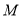 点表示的数是 ,则
点表示的数是 ,则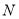 点表示的数是 .
点表示的数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市拟购进甲乙两种大米,购进计划见下表:
品种
项目
数量
(单位:kg)
进价
(单位:元/kg)
售价的设定标准
甲种大米
600
a
在进价的基础上提高40%
乙种大米
800
b
在进价的基础上提高30%
(1)若计划购进的大米全部售出,超市可获利多少元?(用含有a,b的代数式表示结果)
(2)由于包装袋破损,两种大米混合在一起,无法分装,超市决定以散装米出售,售价为
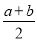 元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由?
元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售
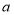 元,在果园每千克售
元,在果园每千克售 元
元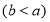 .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用
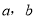 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.(2)若
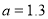 元,
元,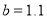 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批A、B两型号节能灯,已知2只A型节能灯和3只B型节能灯共需31元;1只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共100只,并且A型节能灯的数量不多于B型节能灯数量的2倍,请设计出最省钱的购买方案.
相关试题

