【题目】材料1:反射定律
当入射光线AO照射到平面镜上时,将遵循平面镜反射定律,即反射角(∠BOM)的大小等于入射角(∠AOM)的大小,显然,这两个角的余角也相等,其中法线(OM)与平面镜垂直,并且满足入射光线、反射光线(OB)与法线在同一个平面.
材料2:平行逃逸角
对于某定角∠AOB=α(0°<α<90°),点P为边OB上一点,从点P发出一光线PQ(射线),其角度为∠BPQ=β(0°<β<90°),当光线PQ接触到边OA和OB时会遵循反射定律发生反射,当光线PQ经过n次反射后与边OA或OB平行时,称角为定角α的n阶平行逃逸角,特别地,当光线PQ直接与OA平行时,称角β为定角α的零阶平行逃逸角.
(1)已知∠AOB=α=20°,
①如图1,若PQ∥OA,则∠BPQ= °,即该角为α的零阶平行逃逸角;
②如图2,经过一次反射后的光线P1Q∥OB,此时的∠BPP1为α的平行逃逸角,求∠BPP1的大小;
③若经过两次反射后的光线与OA平行,请补全图形,并直接写出α的二阶平行逃逸角为 °;
(2)根据(1)的结论,归纳猜想对于任意角α(0°<α<90°),其n(n为自然数)阶平行逃逸角β= (用含n和a的代数式表示).

参考答案:
【答案】(1)①20;②∠BPP1=40°③60°;(2)(n+1)α.
【解析】
(1)①两直线平行,同位角相等;②由“反射定律”可得∠AP1Q=∠PP1O,再由P1Q∥OB可得∠AP1Q=∠PP1O=∠AOB=20°;③先作PQ∥AO,再根据“反射定律”先画出P2P1,再画出P1P.
(3)分别从零阶、一阶、二阶逃逸角与∠α的关系中归纳一般性关系.
解:(1)①如图①中,∵PQ∥OA,
∴∠BPQ=∠AOB=20°,
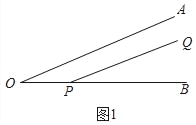
故答案为20.
②如图2中,
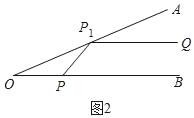
∵P1Q∥OB,
∴∠AP1Q=∠PP1O=∠AOB=20°,
∴∠BPP1=∠AOB+∠PP1O=40°.
③如图3中,如图所示,α的二阶平行逃逸角为20°×3=60°,
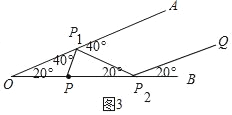
(2)由(1)可知:α的零阶平行逃逸角为α,α的1阶平行逃逸角为2α,α的二阶平行逃逸角为3α,
…,由此可以推出,α的n阶平行逃逸角为(n+1)α,
故答案为(n+1)α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.

(1)求A,B两点的坐标;
(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,问:
①若△PBO的面积为S,求S关于a的函数解析式;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
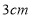 B.
B. 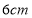 C.
C.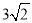
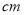 D.
D. 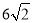
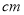

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分为四类(A.特别好,B.好,C.一般,D.较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:
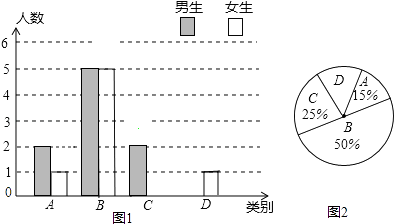
(1)本次调查中,王老师一共调查了名学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)假定全校各班实施新课程改革效果一样,全校共有学生2 400人,请估计该校新课程改革效果达到A类的有多少学生;
(4)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店第一次用400元购进胶皮笔记本若干个,第二次又用400元购进该种型号的笔记本,但这次每个的进价是第一次进价的1.25倍,购进数量比第一次少了20个.
(1)求第一次每个笔记本的进价是多少?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后后获利不低于460元,问每个笔记本至少是多少元?
相关试题

