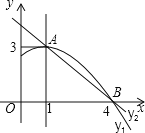
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1,
其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
参考答案:
【答案】C
【解析】
试题分析:根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据顶点坐标对③进行判断;根据抛物线的对称性对④进行判断;根据函数图象得当1<x<4时,一次函数图象在抛物线下方,则可对⑤进行判断.
解:∵抛物线的顶点坐标A(1,3),
∴抛物线的对称轴为直线x=﹣![]() =1,
=1,
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(﹣2,0),所以④错误;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以⑤正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,E是AB的中点,CE=DE.
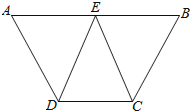
(1)求证:∠AED=∠BEC;
(2)连接AC、BD,求证:AC=BD.
-
科目: 来源: 题型:
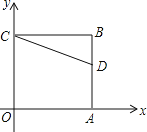
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知:(x﹣3)2
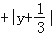 =0,求3x2y﹣[2xy2﹣2(xy﹣
=0,求3x2y﹣[2xy2﹣2(xy﹣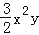 )+3xy]+5xy2的值.
)+3xy]+5xy2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面三组数中是勾股数的一组是( )
A. 7,8,9 B. 3,4,5 C. 1.5,5,2.5 D. 20,28,35
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的每个外角是 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】和数轴上的点一一对应的数是( )
A. 整数 B. 有理数 C. 实数 D. 无理数
相关试题

