【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
参考答案:
【答案】 (1)4 (2) ![]() ,
, ![]() ) (3)
) (3) ![]()
![]()
![]()
![]()
【解析】根据已知代数式为自然数,确定出x的值即可;
(2)用x表示出y,确定出方程的正整数解即可;
(3)用x表示出y,确定出方程的整数解即可.
解:(1)由题意得:x2=1,x2=2,x2=3,x2=6,
解得:x=3,x=4,x=5,x=8,共4个;
故答案为:4;
(2)方程整理得:y=2x+5,
当x=1时,y=3;当x=2时,y=1,
则方程的正整数解为![]() ,
, ![]() ;
;
故答案为: ![]() ,
, ![]()
(3)根据题意得:y=![]() ,
,
根据题意得:x+3=1,x+3=2,x+3=4,x+3=8,
解得:x=2,x=1,x=1,x=5,
相应的y=8,y=4,y=2,y=1,
∴它的所有整数解为![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
 将下表填写完整:
将下表填写完整:平均数
中位数
方差
甲
______
8
______
乙
8
______
2
 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么? 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______ 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.

(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化肥厂去年四月份生产化肥500吨,因管理不善,五月份的产量减少了
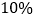 ,从六月起强化管理,该厂产量逐月上升,七月份产量达到648吨.
,从六月起强化管理,该厂产量逐月上升,七月份产量达到648吨. 该厂五月份的产量为______吨;
该厂五月份的产量为______吨;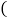 直接填结果
直接填结果
 求六、七两月产量的平均增长率.
求六、七两月产量的平均增长率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.

(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:
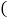 画出图形,把截去的部分打上阴影
画出图形,把截去的部分打上阴影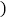
 新多边形内角和比原多边形的内角和增加了
新多边形内角和比原多边形的内角和增加了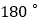 .
. 新多边形的内角和与原多边形的内角和相等.
新多边形的内角和与原多边形的内角和相等. 新多边形的内角和比原多边形的内角和减少了
新多边形的内角和比原多边形的内角和减少了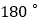 .
. 将多边形只截去一个角,截后形成的多边形的内角和为
将多边形只截去一个角,截后形成的多边形的内角和为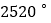 ,求原多边形的边数.
,求原多边形的边数.
相关试题

