【题目】已知,矩形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),已知直线AC与双曲线y=![]() (m≠0)在第一象限内有一交点Q(5,n).
(m≠0)在第一象限内有一交点Q(5,n).
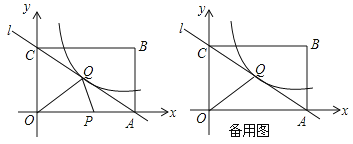
(1)求直线AC和双曲线的解析式;
(2)若动点P从A点出发,沿折线AO→OC的路径以每秒2个单位长度的速度运动,到达C处停止.求△OPQ的面积S与的运动时间t秒的函数关系式,并求当t取何值时S=10.
参考答案:
【答案】(1)直线AC的解析式为:![]() ,双曲线为:
,双曲线为:![]() ;(2)
;(2)![]() ,当t=2.5秒或t=7秒时,S=10.
,当t=2.5秒或t=7秒时,S=10.
【解析】
(1)设直线![]() 的解析式为
的解析式为![]() .将
.将![]() 、
、![]() 两点代入其中,即利用待定系数法求一次函数解析式;然后利用一次函数图象上点的坐标特征,将点
两点代入其中,即利用待定系数法求一次函数解析式;然后利用一次函数图象上点的坐标特征,将点![]() 代入函数关系式求得
代入函数关系式求得![]() 值;最后将
值;最后将![]() 点代入双曲线的解析式,求得
点代入双曲线的解析式,求得![]() 值,即可求得双曲线的解析式;
值,即可求得双曲线的解析式;
(2)分类讨论:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
解:(1)设直线![]() 的解析式为
的解析式为![]() ,过
,过![]() 、
、![]() ,
,
![]() ,
,
解得: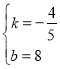 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
又![]() 在直线
在直线![]() 上,
上,
![]() ,
,
又![]() 双曲线
双曲线![]() 过
过![]() ,
,
![]() ,
,
![]() 双曲线的解析式为:
双曲线的解析式为:![]() ;
;
(2)当![]() 时,
时,![]() ,
,
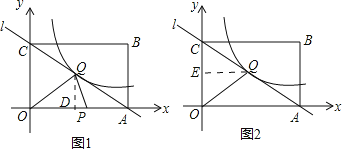
过![]() 作
作![]() ,垂足为
,垂足为![]() ,如图1,
,如图1,
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]()
解得![]() ,
,
当![]() 时,
时,![]() ,
,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,如图2
,如图2
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,
综上,![]() ,
,
当![]() 秒时,
秒时,![]() 的面积不存在,
的面积不存在,
![]() 当
当![]() 秒或
秒或![]() 秒时,
秒时,![]() .
.
-
科目: 来源: 题型:
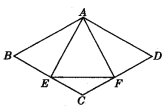
查看答案和解析>>【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,
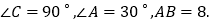 点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒
点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒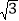 个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.(1)用含t的代数式表示线段AQ的长.
(2)当点P在线段AB上运动时,求PQ与△ABC一边垂直时t的值.
(3)设△APQ的面积为S(S>0),求S与t的函数关系式.
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .数轴上表示-12和-6的两点之间的距离是 .
(2)数轴上表示x和-4的两点之间的距离表示为 .
(3)|x-2|+|x+4|的最小值为 时,能使|x-2|+|x+4|取最小值的所有整数x的和是 .
(4)若数轴上两点A、B对应的数分别是-1、3,现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,当点A与点B之间的距离为3个单位长度时,求点A所对应的数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点0为直线AB上一点,∠AOC=50
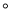 ,OD平分∠AOC,∠DOE=90
,OD平分∠AOC,∠DOE=90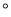 .
.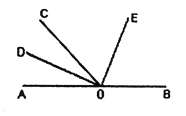
(1)请你数一数,图中有多少个小于平角的角:
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=2,平移距离为3,则阴影部分的面积是_____.
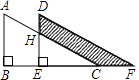
-
科目: 来源: 题型:
查看答案和解析>>【题目】①将下列各数填入相应的括号中:
0,-2019,7.01,+6,+30﹪,
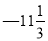
负数:{ }
正数:{ }
整数:{ }
②.画一条数轴,在数轴上标出以下各点,然后用“<”符号连起来.
-
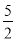 ;-(-4);-|-1|;
;-(-4);-|-1|;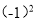 ;0;
;0;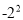 ;2.5;
;2.5;
相关试题

