【题目】综合题。
(1)先化简,再求代数式的值( ![]() +
+ ![]() )÷
)÷ ![]() ,其中a=(﹣1)2012+tan60°.
,其中a=(﹣1)2012+tan60°.
(2)关于x的方程3x2+mx﹣8=0有一个根是 ![]() ,求另一个根及m的值.
,求另一个根及m的值.
参考答案:
【答案】
(1)解:a=1+ ![]() ,
,
∴原式= ![]() ×
× ![]() +
+ ![]() ×
× ![]()
= ![]() +
+ ![]()
= ![]()
= ![]()
= ![]()
(2)解:设另外一根为x,
由根与系数的关系可知: ![]() x=﹣
x=﹣ ![]() ,
,
∴x=﹣4,
∴﹣4+ ![]() =﹣
=﹣ ![]() ,
,
∴m=10
【解析】(1)先化简原式,然后将a的值化简即可求出答案.(2)根据根与系数的关系即可求出m的值.
【考点精析】本题主要考查了根与系数的关系和特殊角的三角函数值的相关知识点,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
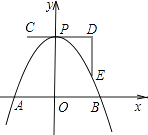
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2﹣13+8;
(2)2+(﹣6)÷2×
 ;
;(3)5×22﹣3÷(﹣
 );
);(4)﹣42+(﹣9)×[(﹣2)3+
 ]
] -
科目: 来源: 题型:
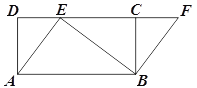
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
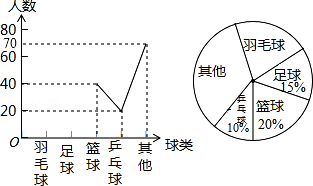
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
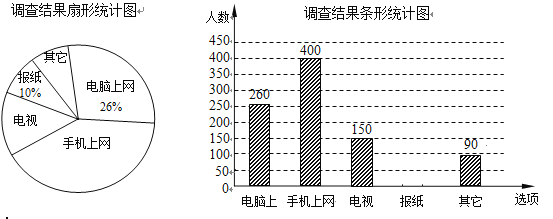
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
相关试题

