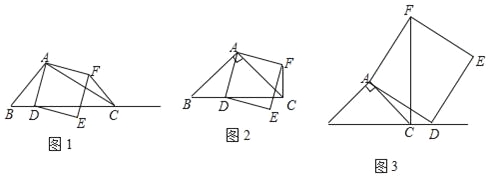
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
参考答案:
【答案】(1)①△ACF,垂直,相等
②结论是否仍然成立,理由见解析
(2)当∠ACB=45°时,CF⊥BC,理由见解析
【解析】
试题分析:解题的关键是过点A作AG⊥AC交CB的延长线于点G,构造全等三角形.(1)①当点D在线段BC上时,根据等腰直角三角形的性质以及旋转的性质,即可得出CF=BD,BD⊥CF;②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD,结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°,即CF⊥BD;
(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①中的方法可得CF⊥BD.
解:(1)①如图2所示,将△ABD绕A点逆时针旋转90°,所得到△ACF,则
由旋转的性质可得:∠ACF=∠B,CF=BD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°=∠ACF,
∴∠BCF=90°,即BD⊥CF;
故答案为:△ACF,垂直,相等;
②如图3所示,当点D在BC的延长线上时,①中的结论仍成立.
证明:由正方形ADEF得,AD=AF,∠DAF=90°.
∵∠BAC=90°
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC(SAS),
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,即 CF⊥BD;
(2)如图4所示,当∠ACB=45°时,CF⊥BD.
理由:过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB=45°,
∴∠ACB=∠AGC,
∴AC=AG,
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.相等的角是对顶角
B.两条不相交的线段是平行的
C.过一点有且只有一条直线与已知直线平行
D.互为邻补角的两角的角平分线互相垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对部分参加研学旅行社会实践活动的中学生的年龄(单位:岁)进行统计,结果如表:
年龄
12
12
14
15
16
人数
1
2
2
3
1
则这些学生年龄的众数和中位数分别是( )
A. 15,14B. 15,13C. 14,14D. 13,14
-
科目: 来源: 题型:
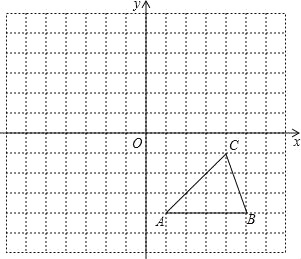
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米)
运费(元/斤·千米)
甲养殖场
200
0.012
乙养殖场
140
0.015
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义新运算“※”,对任意有理数a、b,规定a※b=ab+a﹣b,
例如:1※2=1×2+1﹣2=1,(1)求3※(﹣5)的值;
(2)若(-3)※b与b,互为相反数,求b的值.
相关试题

