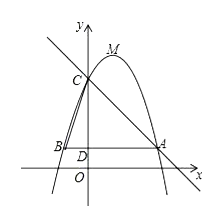
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.

参考答案:
【答案】(1)y=﹣(x﹣2)2+12,M(2,12)
(2)S△ABC=15
(3)6<m<9
【解析】
试题分析:(1)把点A、C的坐标代入函数解析式,用待定系数法求出抛物线解析式;
(2)结合点A、B、C的坐标,三角形的面积公式进行解答;
(3)点M是沿着对称轴直线x=2向下平移的,可先求出直线AC的解析式,将x=2代入求出点M在向下平移时与AC、AB相交时y的值,即可得到m的取值范围.
解:(1)把点A(5,3),点C(0,8)代入二次函数y=﹣x2+bx+c,得
![]() ,
,
解得![]() ,
,
∴二次函数解析式为y=﹣x2+4x+8,配方得y=﹣(x﹣2)2+12
∴点M的坐标为(2,12);
(2)由(1)知,抛物线的对称轴是x=2.
∵A(5,3),AB∥x轴,
∴AB=6,D(0,3)
∵C(0,8),
∴CD=5,
∴△ABC的面积=![]() ABCD=
ABCD=![]() ×6×5=15,
×6×5=15,
即△ABC的面积=15;
(3)设直线AC解析式为y=kx+b,把点A(5,3),C(0,8)代入![]() ,
,
解得![]() ,
,
∴直线AC的解析式为y=﹣x+8,对称轴直线x=2与△ABC两边分别交于点E、点F,
把x=2代入直线AC解析式y=﹣x+8,
解得y=6,则点E坐标为(2,6),点F坐标为(2,3)
∴3<12﹣m<6,解得6<m<9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标为(3,-2),则点A向右平移3个单位后的坐标为( )
A. (0,-2) B. (6,-2) C. (3,1) D. (3,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8)
B.(1,﹣2)
C.(﹣6,﹣1)
D.(0,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.相等的角是对顶角
B.两条不相交的线段是平行的
C.过一点有且只有一条直线与已知直线平行
D.互为邻补角的两角的角平分线互相垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校对部分参加研学旅行社会实践活动的中学生的年龄(单位:岁)进行统计,结果如表:
年龄
12
12
14
15
16
人数
1
2
2
3
1
则这些学生年龄的众数和中位数分别是( )
A. 15,14B. 15,13C. 14,14D. 13,14
-
科目: 来源: 题型:
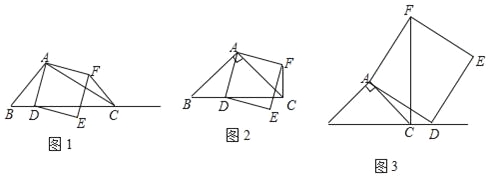
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
-
科目: 来源: 题型:
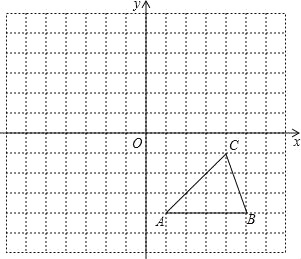
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1.
相关试题

