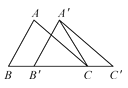
【题目】如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .
参考答案:
【答案】12.
【解析】根据平移性质,判定△A′B′C为等边三角形,然后求解.
解:由题意,得BB′=2,
∴B′C=BC-BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴△A′B′C的周长=3A′B′=12.
故答案为:12.
“点睛”本题考查的是平移的性质,熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强青少年的防毒拒毒意识,学校举办了一次“禁毒教育”演讲比赛,其中某位选手的演讲内容、语言表达、演讲技巧这三项得分分别为90分,80分,85分,若依次按50%,30%,20%的比例确定成绩,则该选手的最后得分是__________分.
-
科目: 来源: 题型:
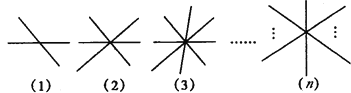
查看答案和解析>>【题目】(1)两条直线相交于一点有2组不同的对顶角;
(2)三条直线相交于一点有6组不同的对顶角;
(3)四条直线相交于一点有12组不同的对顶角;
(4)n条直线相交于同一点有___________组不同对顶角.(如图所示)
-
科目: 来源: 题型:
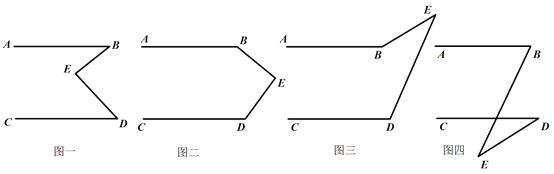
查看答案和解析>>【题目】有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
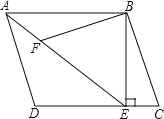
(1)求证:△ABF∽△EAD;
(2)若AD=3,∠BAE=30°,求BF的长.(计算结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中属于定义的是( )
A. 直角都相等
B. 作已知角的平分线
C. 连接两点的线段的长度,叫做这两点间的距离
D. 两点之间,线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(2a+2b+1)(2a+2b-1)=63,那么a+b的值为________.
相关试题

