搜索
【题目】如图是某超市地下停车场入口的设计图，请根据图中数据计算CE的长度．（结果保留小数点后两位；参考数据：sin22°=0.3746，cos22°=0.9272，tan22°=0.4040） 
参考答案：
【答案】解：由已知有：∠BAE=22°，∠ABC=90°，∠CED=∠AEC=90° ∴∠BCE=158°，
∴∠DCE=22°，
又∵tan∠BAE= 
，
∴BD=ABtan∠BAE，
又∵cos∠BAE=cos∠DCE= 
，
∴CE=CDcos∠BAE
=（BD﹣BC）cos∠BAE
=（ ABtan∠BAE﹣BC）cos∠BAE
=（10×0.4040﹣0.5）×0.9272
≈3.28（m）
【解析】通过解Rt△BAD求得BD=ABtan∠BAE，通过解Rt△CED求得CE=CDcos∠BAE．然后把相关角度所对应的函数值和相关的线段长度代入进行求值即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数y=ax2+1与y=
（a≠0）在同一平面直角坐标系中的图象可能是（ ）
A.
B.
C.
D.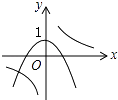
-
科目： 来源： 题型：
查看答案和解析>>【题目】经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．
（1）请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果；
（2）求这两辆汽车都向左转的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】 已知△ABC中，∠A=25°，∠B=40°．
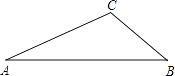
（1）求作：⊙O，使得⊙O经过A、C两点，且圆心O落在AB边上．（要求尺规作图，保留作图痕迹，不必写作法）
（2）求证：BC是（1）中所作⊙O的切线． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
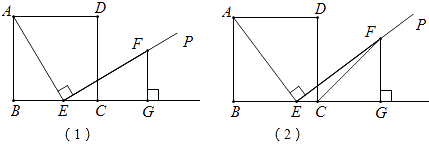
（1）求证：FG=BE；
（2）连接CF，如图（2），求证：CF平分∠DCG；
（3）当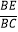
= 
时，求sin∠CFE的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），抛物线y=﹣
x2+x+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（﹣2，0）．
（1）求此抛物线的解析式；
（2）①若点D是第一象限内抛物线上的一个动点，过点D作DE⊥x轴于E，连接CD，以OE为直径作⊙M，如图（2），试求当CD与⊙M相切时D点的坐标；
②点F是x轴上的动点，在抛物线上是否存在一点G，使A、C、G、F四点为顶点的四边形是平行四边形？若存在，求出点G的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现在两辆汽车经过这个十字路口．
（1）请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果；
（2）求这两辆汽车都向左转的概率．
相关试题
