【题目】已知等边三角形ABC,点D是边AC上任意一点,延长BC至E,使CE=AD.
(1)如图1,点D是AC中点,求证:DB=DE;
(2)如图2,点D不是AC中点,求证:DB=DE;
(3)如图3,点D不是AC中点,点F是BD的中点,连接AE,AF,求证:AE=2AF.

参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据等边三角形的性质得到BD为∠ABC的角平分线,∠ABC=∠ACB=60°,根据等腰三角形的性质、等腰三角形的判定定理证明;
(2)过D作EF∥DG交AB,交BC于G,证明△BDC≌△EDG,根据全等三角形的性质证明结论;
(3)延长AF至H,使FH=AF,连接DH,证明△ABF≌△HDF,得到AB=HD,∠ABF=∠HDF,证明△ADH≌△ECA,得到AE=AH,证明结论.
证明:(1)∵在等边△ABC中,D是AC的中点,
∴BD为∠ABC的角平分线,∠ABC=∠ACB=60°,
∴![]()
∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE+∠CED=∠ACB,
∴![]()
∴∠CBD=∠CED=30°,
∴BD=DE;
(2)过D作EF∥DG交AB,交BC于G
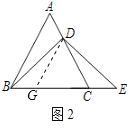
∴∠DGC=∠ABC=60°,又∠DCG=60°,
∴△DGC为等边三角形,
∴DG=GC=CD,
∴BC﹣GC=AC﹣AD,即AD=BG,
∵AD=CE,
∴BG=CE,
∴BC=GE,
在△BDC和△EDG中,
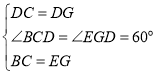 ,
,
∴△BDC≌△EDG(SAS)
∴BD=DE;
(3)延长AF至H,使FH=AF,连接DH,

在△ABF和△HDF中,
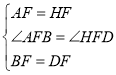 ,
,
∴△ABF≌△HDF(SAS)
∴AB=HD,∠ABF=∠HDF,
∴AC=HD,AB∥DH,
∴∠ADH=180°﹣∠BAC=120°,
在△ADH和△ECA中,
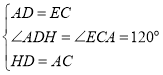
∴△ADH≌△ECA(SAS)
∴AE=AH,
∵AH=2AF,
∴AE=2AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽均为
 的纸条,交叉叠放在一起,且它们的交角为
的纸条,交叉叠放在一起,且它们的交角为 ,则它们重叠部分的面积为( )
,则它们重叠部分的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
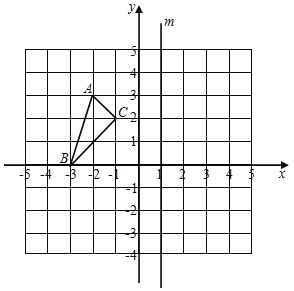
查看答案和解析>>【题目】如图所示的平面直角坐标系中,直线m上各点的横坐标都为1(记作直线x=1),A,B,C三点的坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,2).
(1)画出△ABC关于直线x=1对称的△A1B1C1并写出A1,B1,C1的坐标.
(2)若△ABC内部有一点H(﹣2,b),求点H关于直线x=a对称的点H1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有
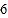 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为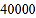 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为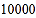 个.
个. 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率; 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“绿色出行”的号召,小王上班由自驾车改为乘坐公交车.已知小王家距离上班地点
 ,他乘坐公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的
,他乘坐公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的 倍还多
倍还多 .他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的
.他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的 .
.(1)小王用自驾车上班平均每小时行驶多少千米?
(2)上周五,小王上班时先步行了
 ,然后乘公交车前往,共用
,然后乘公交车前往,共用 小时到达.求他步行的速度.
小时到达.求他步行的速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
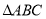 中,点
中,点 是
是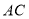 边上的一个动点,过点
边上的一个动点,过点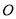 作直线
作直线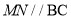 ,设
,设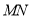 交
交 的角平分线于点
的角平分线于点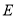 ,交
,交 的外角平分线于点
的外角平分线于点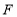 .
.(1)求证:
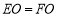 ;
;(2)当点
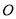 运动到何处时,四边形
运动到何处时,四边形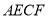 是矩形?并证明你的结论.
是矩形?并证明你的结论.(3)当点
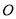 运动到何处,且
运动到何处,且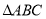 满足什么条件时,四边形
满足什么条件时,四边形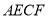 是正方形?并说明理由.
是正方形?并说明理由.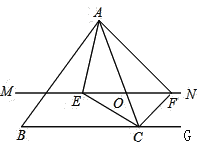
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,已知
中,已知 ,
, ,对角线
,对角线 平分
平分 ,
, ,
, ,则边
,则边 的长度为________.
的长度为________.
相关试题

